
【题目】已知函数![]() (
(![]() ).
).
(1)![]() 为
为![]() 的导函数,讨论
的导函数,讨论![]() 的零点个数;
的零点个数;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了![]() 名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为选手成绩“优秀”与文化程度有关?
的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
(2)若参赛选手共![]() 万人,用频率估计概率,试估计其中优秀等级的选手人数;
万人,用频率估计概率,试估计其中优秀等级的选手人数;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》由如下问题:“今有金箠,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.问次一尺各重几何?”意思是:“现有一根金杖,长5尺,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”设该金杖由粗到细是均匀变化的,其重量为![]() ,现将该金杖截成长度相等的10段,记第
,现将该金杖截成长度相等的10段,记第![]() 段的重量为
段的重量为![]() ,且
,且![]() ,若
,若![]() ,则
,则![]() ( )
( )
A. 6 B. 5 C. 4 D. 7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x﹣y=1与圆Γ:x2+y2﹣2x+2y﹣1=0相交于A,C两点,点B,D分别在圆Γ上运动,且位于直线l的两侧,则四边形ABCD面积的最大值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
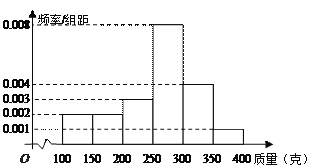
(1) 试估计这组数据的众数、中位数、平均数;
(2)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所有芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某机构调查小学生课业负担的情况,设平均每人每天做作业时间为X(单位:分钟),按时间分下列四种情况统计:①0~30分钟;②30~60分钟;③60~90分钟;④90分钟以上,有1000名小学生参加了此项调查,如图是此次调查中某一项的程序框图,其输出的结果是600,则平均每天做作业时间在0~60分钟内的学生的频率是( )

A. 0.20B. 0.80C. 0.60D. 0.40
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的表面积为( ) 
A.8+8 ![]() +4
+4 ![]()
B.8+8 ![]() +2
+2 ![]()
C.2+2 ![]() +
+ ![]()
D.![]() +
+ ![]() +
+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知⊙O:x2+y2=6,P为⊙O上动点,过P作PM⊥x轴于M,N为PM上一点,且 ![]() . (Ⅰ)求点N的轨迹C的方程;
. (Ⅰ)求点N的轨迹C的方程;
(Ⅱ)若A(2,1),B(3,0),过B的直线与曲线C相交于D、E两点,则kAD+kAE是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com