
【题目】已知点(1,2)是函数f(x)=ax(a>0,且a≠1)的图象上一点,数列{an}的前n项和Sn=f(n)﹣1.
求数列{an}的通项公式.
【答案】解:把点(1,2)代入函数f(x)=ax , 得a=2.
∴Sn=f(n)﹣1=2n﹣1,
当n=1时,a1=S1=21﹣1=1,
当n≥2时,an=Sn﹣Sn﹣1=(2n﹣1)﹣(2n﹣1﹣1)=2n﹣1 ,
经验证可知n=1时,也适合上式,
∴an=2n﹣1 .
【解析】把点(1,2)代入函数f(x)=ax , 得a=2.可得:Sn=f(n)﹣1=2n﹣1,利用递推关系即可得出.
【考点精析】根据题目的已知条件,利用等比数列的通项公式(及其变式)和数列的通项公式的相关知识可以得到问题的答案,需要掌握通项公式:![]() ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】如图是绵阳市某小区100户居民2014年平均用水量(单位:t)的频率分布直方图,则该小区2014年的月平均用水量的众数,中位数的估计值分别是( ) 
A.2,2.5
B.2,2.02
C.2.25,2.5
D.2.25,2.02
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四边形ABCD中, ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3).
=(﹣2,﹣3). 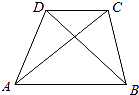
(1)若 ![]() ∥
∥ ![]() ,求x与y满足的关系式;
,求x与y满足的关系式;
(2)满足(1)的同时又有 ![]() ⊥
⊥ ![]() ,求x,y的值.
,求x,y的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在正项等比数列{an}中,a1=1,a2a4=16,则|a1﹣12|+|a2﹣12|+…+|a8﹣12|=( )
A.224
B.225
C.226
D.256
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:点P在直径AB=1的半圆上移动(点P不与A,B重合),过P作圆的切线PT且PT=1,∠PAB=α,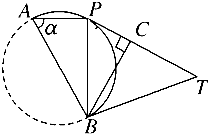
(1)当α为何值时,四边形ABTP面积最大?
(2)求|PA|+|PB|+|PC|的取值范围?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合 ![]() ,B={x|2<x<9}.
,B={x|2<x<9}.
(1)分别求:R(A∩B),(RB)∪A;
(2)已知C={x|2a<x<a+3},若CB,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com