
分析 利用平方差法:设P1(x1,y1),P2(x2,y2),代入双曲线方程然后作差,由中点坐标公式及斜率公式可求得直线l的斜率,再用点斜式即可求得直线方程.
解答 解:设P1(x1,y1),P2(x2,y2),则x1+x2=2,y1+y2=8,
代入双曲线方程,两式相减得$\frac{1}{4}$(x1+x2)(x1-x2)-$\frac{1}{16}$(y1+y2)(y1-y2)=0
∴$\frac{1}{2}$(x1-x2)-$\frac{1}{2}$(y1-y2)=0
∴k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=1,
故所求直线方程为y-4=x-1,即x-y+3=0.
故答案为:x-y+3=0.
点评 本题考查直线与圆锥曲线的位置关系,考查直线方程的求法,涉及弦中点问题,往往考虑利用“平方差法”加以解决.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
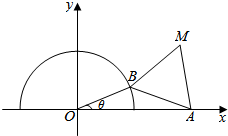 如图,已知半圆O:x2+y2=1(y≥0)及点A(2,0),B为半圆周上任意一点,以AB为一边作等边△ABM.设∠AOB=θ,其中0<θ<π.
如图,已知半圆O:x2+y2=1(y≥0)及点A(2,0),B为半圆周上任意一点,以AB为一边作等边△ABM.设∠AOB=θ,其中0<θ<π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{1}{2},+∞)$ | B. | $[-\frac{1}{2},2)$ | C. | $(-∞,-\frac{1}{2}]$ | D. | (-3,$-\frac{1}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com