
| A. | 4π | B. | 8π | C. | 16π | D. | 32π |
分析 如图,取BC中点D,连结AD、PD,过A作AH⊥PD于D,易知AH⊥面PBC,
即∠APD就是直线PA与平面PBC所成角,由tan∠APD=$\frac{AD}{AP}=\frac{1}{2}$,得AP
以AB,AC,AP为棱的长方体的外接球就是三棱锥P-ABC的外接球,即可求出半径.
解答 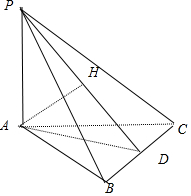 解:如图,取BC中点D,连结AD、PD,
解:如图,取BC中点D,连结AD、PD,
∵AB=AC,∴AD⊥BC,由因为PA⊥面ABC,∴BC⊥面PAD,
过A作AH⊥PD于D,易知AH⊥面PBC,
∴∠APD就是直线PA与平面PBC所成角,∴tan∠APD=$\frac{AD}{AP}=\frac{1}{2}$,
∵AD=$\frac{1}{2}BC=\frac{\sqrt{2}}{2}$,∴$PA=\sqrt{2}$.
∵AB,AC,AP相互垂直,∴以AB,AC,AP为棱的长方体的外接球就是三棱锥P-ABC的外接球,
∴三棱锥P-ABC的外接球的半径R=$\frac{\sqrt{{1}^{2}+{1}^{2}+(\sqrt{2})^{2}}}{2}=1$,三棱锥P-ABC的外接球的表面积为4πR2=4π;
故选:A.
点评 本题考查了三棱锥的外接球,转化已知求出球的半径是关键,属于中档题.


科目:高中数学 来源: 题型:解答题
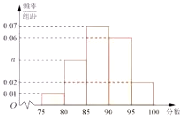 某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100],规定90分及以上为合格:
某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100],规定90分及以上为合格:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-∞,-1)∪(1,+∞) | C. | [-1,1] | D. | (-∞,-1]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校在市统测后,从高三年级的1000名学生中随机抽出100名学生的数学成绩作为样本进行分析,得到样本频率分布直方图,如图所示.则估计该校高三学生中数学成绩在[110,140)之间的人数为660.
某校在市统测后,从高三年级的1000名学生中随机抽出100名学生的数学成绩作为样本进行分析,得到样本频率分布直方图,如图所示.则估计该校高三学生中数学成绩在[110,140)之间的人数为660.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com