
����Ŀ����ij�и�����ѧ��������У�ȫ�й���![]() ��ѧ���μ��˱��ο��ԣ�����ʾ���Ը��вμӿ���ѧ������Ϊ
��ѧ���μ��˱��ο��ԣ�����ʾ���Ը��вμӿ���ѧ������Ϊ![]() �ˣ���ʾ���Ը��вμӿ���ѧ������Ϊ
�ˣ���ʾ���Ը��вμӿ���ѧ������Ϊ![]() ��.�ִ����вμӿ��Ե�ѧ���������ȡ
��.�ִ����вμӿ��Ե�ѧ���������ȡ![]() �ˣ������ɼ����ݷ���.
�ˣ������ɼ����ݷ���.

��1����ƺ����ij���������˵�������������������ɼ��ɣ���
��2������![]() �˵���ѧ�ɼ���������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���ݴ˹��Ʊ��μ��ȫ��ѧ����ѧ�ɼ���ƽ���֣�
�˵���ѧ�ɼ���������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���ݴ˹��Ʊ��μ��ȫ��ѧ����ѧ�ɼ���ƽ���֣�
���𰸡���1������������2��92.4
��������
��1����������IJ�����ѡ��ֲ�������ٽ�ϳ����ȼ������ʾ���Ը��к�ʾ���Ը�������ȡ��������
��2����ÿ�����εױߵ��е�ֵ������Ӧ���ε�������ý������ȫ����ӿɵó����β���ȫ��ѧ����ѧ�ɼ���ƽ���֡�
��1���������������Բ���������ֹ��ɣ��ʲ��÷ֲ������
�����⣬��ʾ���Ը��г�ȡ![]() �ˣ�
�ˣ�
�ӷ�ʦ���Ը��г�ȡ![]() �ˣ�
�ˣ�
��2����Ƶ�ʷֲ�ֱ��ͼ��������ƽ����Ϊ
![]()
�Ʋ���Ʊ��μ��ȫ��ѧ����ѧƽ����Ϊ![]()


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC���̣�![]() +
+![]() =1��a��b��0����M��x0 �� y0������ԲC������һ�㣬F��c��0������Բ���ҽ��㣮
=1��a��b��0����M��x0 �� y0������ԲC������һ�㣬F��c��0������Բ���ҽ��㣮
��1������Բ��������Ϊe��֤��|MF|=a��ex0��
��2����֪��������F��ֱ��l��Բx2+y2=b2�����ڵ�Q��������ԲC����A��B���㣬��A��B���㶼��y����Ҳ࣬��a=2�����ABF���ܳ���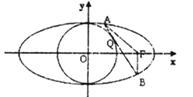
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ����ƽ������
����ƽ������![]() Ϊֱ����Բ����ƽ�洹ֱ��
Ϊֱ����Բ����ƽ�洹ֱ��![]() Ϊ
Ϊ![]() �е㣬
�е㣬![]() ��Բ����һ�㣬��
��Բ����һ�㣬��![]() ��
��![]() ��
��![]() ��
��

��1��������ֱ��![]() ��
��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
��2�����![]() ���߶�
���߶�![]() �ϵĵ㣬������
�ϵĵ㣬������![]() ����ֱ��
����ֱ��![]() ƽ��
ƽ��![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019�꣬�ӱ���8ʡ�����˸߿��ĸ��ۺϷ�������ȡ��3+1+2��ģʽ�������ġ���ѧ��Ӣ��ؿ���Ȼ����������������ʷ��ѡ��1�ţ�����˼�����Ρ���������ѧ��������ѡ��2��.Ϊ�˸��ý������Ĺ滮����ͬѧ�Ը�һһ�������ߴο��Գɼ�����ͳ�Ʒ�����������������ʷ�ɼ��ľ�Ҷͼ��ͼ��ʾ.

(1)����ͬѧ���ѡ��3�Ź��Σ�����ѡ���������������Ź��εĸ��ʣ�
(2)�Ը��ݾ�Ҷͼ������ͬѧӦ����������ʷ��ѡ����һ��ѧ�ƣ���˵�����ɣ�
(3)��ͬѧ���֣����������Գɼ�![]() (��)��༶ƽ����
(��)��༶ƽ����![]() (��)����������ع�ϵ��ͳ���������±���ʾ�����༶ƽ����Ϊ50��ʱ�����������Գɼ�.
(��)����������ع�ϵ��ͳ���������±���ʾ�����༶ƽ����Ϊ50��ʱ�����������Գɼ�.

�����: ![]() ��
��![]() ��
��![]() ��
��![]() .
.
�ο���ʽ��![]() ��
��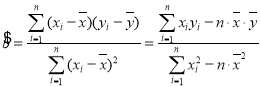 ��
��![]() (����
(����![]() ʱ��ȷ��
ʱ��ȷ��![]() ).
).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ˮ������Ҫ��һ��������ˮ������(ABCD)�ijص�ˮƽ������ˮ�����ܵ�(�ܵ�����Rt��FHE��H��ֱ�����)��������ˮ���ܵ�Խ������ˮ����Ч��Խ�ã����Ҫ��ܵ��Ľӿ�H��AB���е㣬E��F�ֱ������߶�BC��AD�ϣ���֪AB��20�ף�AD��![]() �ף��ǡ�BHE��
�ף��ǡ�BHE��![]() ��
��

��1���Խ���ˮ�����ܵ��ij���L��ʾΪ![]() �ĺ�������д��������
�ĺ�������д��������
��2����![]() ȡ��ֵʱ����ˮ����Ч����ã��������ʱ�ܵ��ij���L��
ȡ��ֵʱ����ˮ����Ч����ã��������ʱ�ܵ��ij���L��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �������ҽ���ֱ�Ϊ
�������ҽ���ֱ�Ϊ![]() ��
��![]() ����
����![]() ��ֱ������Բ����
��ֱ������Բ����![]() ��
��![]() ��������
��������![]() ����
����![]() Ϊֱ�Ƕ���ĵ���ֱ��������������Բ��������Ϊ__________��
Ϊֱ�Ƕ���ĵ���ֱ��������������Բ��������Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ֱ�Ϊ��ABC�����ڽ�A��B��C���Եı߳�����acosB��bcosA= ![]() c��
c��
������ ![]() ��ֵ��
��ֵ��
������A=60�㣬�� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ�����Ϊ![]() �ĺ���
���![]() ����������
���������� ![]() ���� ��
���� ��![]() ����
����![]() ʱ������
ʱ������![]() ���� ��
���� ��![]() ����
����![]() ʱ������
ʱ������![]() �����
�����![]() Ϊ��ƫ�Գƺ��������ָ����ĸ���������
Ϊ��ƫ�Գƺ��������ָ����ĸ���������![]() ����
���� ![]() �� ��
�� ��![]() ����
����![]() .�������ǡ�ƫ�Գƺ������ĺ������Ϊ _______��
.�������ǡ�ƫ�Գƺ������ĺ������Ϊ _______��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com