
【题目】有下列命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则存在唯一实数
,则存在唯一实数![]() ,使得
,使得![]() ;③若
;③若![]() ,则
,则![]() ;④若
;④若![]() ,且
,且![]() 与
与![]() 的夹角为钝角,则
的夹角为钝角,则![]() ;⑤若平面内定点
;⑤若平面内定点![]() 满足
满足![]() ,则
,则![]() 为正三角形.其中正确的命题序号为 ________.
为正三角形.其中正确的命题序号为 ________.
【答案】③⑤
【解析】
①:根据零向量与任一平面向量平行进行判断即可;
②:根据零向量与任一平面向量平行进行判断即可;
③:对已知向量等式进行平方,根据平面向量的运算性质进行求解即可;
④:根据平面向量夹角的坐标表示公式,结合钝角的取值范围进行求解即可;
⑤:根据平面向量加法的几何意义,结合![]() 可以判断出点
可以判断出点![]() 是
是![]() 的重心,再根据平面向量减法的几何意义,结合
的重心,再根据平面向量减法的几何意义,结合![]() ,可以判断出点
,可以判断出点![]() 是
是![]() 的垂心,这样可以确定
的垂心,这样可以确定![]() 的形状.
的形状.
①:当![]() 时,显然满足
时,显然满足![]() ,但是
,但是![]() 不一定成立,故本命题是假命题;
不一定成立,故本命题是假命题;
②:当![]() 时,显然
时,显然![]() 成立,存在实数
成立,存在实数![]() ,使得
,使得![]() ,但是
,但是![]() 不是唯一的,故本命题是假命题;
不是唯一的,故本命题是假命题;
③:因为![]() ,
,
所以![]() ,故本命题是真命题;
,故本命题是真命题;
④:设![]() 与
与![]() 的夹角为
的夹角为![]() ,所以当
,所以当![]() 时,
时,
则有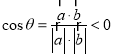 且
且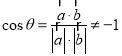 ,
,
即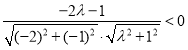 且
且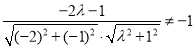 ,
,
解得![]() 且
且![]() ,故本命题是假命题;
,故本命题是假命题;
⑤:因为![]() 所以
所以![]() ,设
,设![]() 中
中![]() 边上的中点为
边上的中点为![]() ,
,
如图所示;
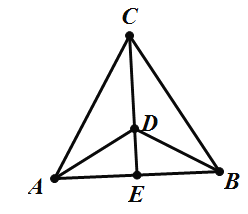
由平面向量的加法的几何意义可知;![]() ,
,
所以![]() ,因此点
,因此点![]() 是
是![]() 的重心.
的重心.
![]() ,
,
因此有![]() ,同理可得
,同理可得![]() ,所以点
,所以点![]() 是
是![]() 的垂心,
的垂心,
因此![]() 为正三角形,故本命题是真命题.
为正三角形,故本命题是真命题.
故答案为;③⑤


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:高中数学 来源: 题型:
【题目】某移动支付公司随机抽取了100名移动支付用户进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)在每周使用移动支付超过3次的样本中,按性别用分层抽样随机抽取5名用户.
①求抽取的5名用户中男、女用户各多少人;
②从这5名用户中随机抽取2名用户,求抽取的2名用户均为男用户的概率.
(2)如果认为每周使用移动支付次数超过3次的用户“喜欢使用移动支付”,能否在犯错误概率不超过0.05的前提下,认为“喜欢使用移动支付”与性别有关?
附表及公式: 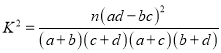
| 0.50 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 0.455 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是

A. 56 B. 60 C. 120 D. 140
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)设命题![]() 实数
实数![]() 满足
满足![]() ,其中
,其中![]() ,命题
,命题![]() 实数
实数![]() 满足
满足![]() .若
.若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
(Ⅱ)已知命题![]() 方程
方程![]() 表示焦点在x轴上双曲线;命题
表示焦点在x轴上双曲线;命题![]() 空间向量
空间向量![]() ,
,![]() 的夹角为锐角,如果命题“
的夹角为锐角,如果命题“![]() ”为真,命题“
”为真,命题“![]() ”为假.求
”为假.求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(Ⅰ)求证:AB∥平面DEG;
(Ⅱ)求二面角C-DF-E的余弦值.
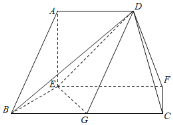
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设等差数列![]() 的公差为
的公差为![]() ,由a3=7,且
,由a3=7,且![]() 、
、![]() 、
、![]() 成等比数列.可得
成等比数列.可得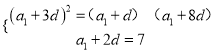 ,解之得即可得出数列
,解之得即可得出数列![]() 的通项公式;
的通项公式;
2)由(1)得![]() ,则
,则![]() ,由裂项相消法可求数列
,由裂项相消法可求数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)设数列![]() 的公差为
的公差为![]() ,且
,且![]() 由题意得
由题意得![]() ,
,
即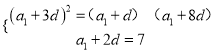 ,解得
,解得![]() ,
,
所以数列![]() 的通项公式
的通项公式![]() .
.
(2)由(1)得![]()
![]() ,
,
![]()
![]() .
.
【题型】解答题
【结束】
18
【题目】四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为正三角形.
为正三角形.
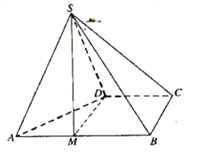
(1)点![]() 为棱
为棱![]() 上一点,若
上一点,若![]() 平面
平面![]() ,
,![]() ,求实数
,求实数![]() 的值;
的值;
(2)求点B到平面SAD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上饶某购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取![]() 张进行统计,将结果分成5组,分别是
张进行统计,将结果分成5组,分别是![]() ,制成如图所示的频率分布直方图(假设消费金额均在
,制成如图所示的频率分布直方图(假设消费金额均在![]() 元的区间内).
元的区间内).

(1)若在消费金额为![]() 元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票均来自
元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票均来自![]() 元区间的概率;
元区间的概率;
(2)为做好五一劳动节期间的商场促销活动,策划人员设计了两种不同的促销方案:
方案一:全场商品打8.5折;
方案二:全场购物满200元减20元,满400元减50元,满600元减80元,满800元减120元,以上减免只取最高优惠,不重复减免.利用直方图的信息分析哪种方案优惠力度更大,并说明理由(直方图中每个小组取中间值作为该组数据的替代值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(2)若![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的值;
的值;
(3)若![]() ,若当
,若当![]() 时,总有
时,总有![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com