
����Ŀ��Ϊ���ռ�����֪ʶ��ǿ������ʶ��ijУ��������רҵ�װ��ȡ60�ˣ�����ʷ���Ұ��ȡ50�˲μӻ���֪ʶ���� ����k2= ![]() ��n=a+b+c+d
��n=a+b+c+d
P��K2��k0�� | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
��1��������Ŀ�����������2��2�����������ݴ��ж����Ƿ���99%�İ�����Ϊ����֪ʶ��רҵ�й�
���� | ������ | �ܼ� | |
�װ� | |||
�Ұ� | 30 | ||
�ܼ� | 60 |
��2��Ϊ�μ��ϼ��ٰ�Ļ���֪ʶ������ѧУ�ٰ�Ԥѡ����Ԥѡ���������100�֣������ͬѧ��60������ͨ��Ԥѡ���������ͬѧ��80������ͨ��Ԥѡ����ÿλͬѧ��60�����ϵĸ���Ϊ ![]() ����80�����ϵĸ���Ϊ
����80�����ϵĸ���Ϊ ![]() ������֪�װ���3�˲μ�Ԥѡ��������1��Ϊ����ѧ�������������X��ʾ�װ�ͨ��Ԥѡ����������X�ķֲ��м�����E��X����
������֪�װ���3�˲μ�Ԥѡ��������1��Ϊ����ѧ�������������X��ʾ�װ�ͨ��Ԥѡ����������X�ķֲ��м�����E��X����
���𰸡�
��1���⣺2��2����������
���� | ������ | �ܼ� | |
�װ� | 40 | 20 | 60 |
�Ұ� | 20 | 30 | 50 |
�ܼ� | 60 | 50 | 110 |
K2= ![]() ��7.8��6.635��
��7.8��6.635��
������99%�İ�����Ϊ����֪ʶ��רҵ�й�
��2���⣺������3��ͬѧΪС����С�ţ�С����С��Ϊ���㣬���¼�M��N��R�ֱ��ʾС����С�ţ�С��ͨ��Ԥѡ����P��M��= ![]() ��P��N��=P��R��=
��P��N��=P��R��= ![]()
�������X��ȡֵΪ0��1��2��3
����P��X=0��=P�� ![]()
![]()
![]() ��=
��= ![]() ��
�� ![]() ��
�� ![]() =
= ![]() ��
��
P��X=1��=P��M ![]()
![]() +
+ ![]() N
N ![]() +
+ ![]()
![]() R��=
R��= ![]() ��
�� ![]() ��
�� ![]() +
+ ![]() ��
�� ![]() ��
�� ![]() +
+ ![]() ��
�� ![]() ��
�� ![]() =
= ![]() ��
��
P��X=2��=P��MN ![]() +
+ ![]() NR+M
NR+M ![]() R��=
R��= ![]() ��
�� ![]() ��
�� ![]() +
+ ![]() ��
�� ![]() ��
�� ![]() +
+ ![]() ��
�� ![]() ��
�� ![]() =
= ![]() ��
��
P��X=3��=P��MNR��= ![]() ��
�� ![]() ��
�� ![]() =
= ![]()
�����������X�ķֲ���Ϊ��
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E��X��=0�� ![]() +1��
+1�� ![]() +2��
+2�� ![]() +3��
+3�� ![]() =
= ![]()
����������1�����������������������������������е����ݣ��õ�K2= ![]() ��7.8��6.635���ɴ˵õ���99%�İ�����Ϊ����֪ʶ������רҵ�йأ���2��������֪X�Ŀ���ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�EX��
��7.8��6.635���ɴ˵õ���99%�İ�����Ϊ����֪ʶ������רҵ�йأ���2��������֪X�Ŀ���ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�EX��


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮΧ�������㼼��������ֳ�ܶȸߡ�����Ч��õ��ص㣮�о�����������ˮΧ��������ʱ��ij������һ���������£�ÿβ���ƽ�������ٶ�![]() ����λ��ǧ��/�꣩����ֳ�ܶ�
����λ��ǧ��/�꣩����ֳ�ܶ�![]() ����λ��β/�����ף��ĺ�������
����λ��β/�����ף��ĺ�������![]() ������
������![]() β/������ʱ��
β/������ʱ�� ![]() ��ֵΪ
��ֵΪ![]() ǧ��/�ꣻ��
ǧ��/�ꣻ��![]() ʱ��
ʱ�� ![]() ��
��![]() ��һ�κ������ҵ�
��һ�κ������ҵ�![]() ʱ��
ʱ�� ![]() ��
��
��![]() ����
����![]() ʱ����
ʱ����![]() ����
����![]() �ĺ����ı���ʽ��
�ĺ����ı���ʽ��
��![]() ������ֳ�ܶ�
������ֳ�ܶ�![]() Ϊ���ʱ��ÿ���������������������λ��ǧ��/�����ף����Դﵽ���������ֵ��
Ϊ���ʱ��ÿ���������������������λ��ǧ��/�����ף����Դﵽ���������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� Sn=n2+2n��bn=anan+1cos��n+1���У�����{bn} ��ǰn���ΪTn �� ��Tn��tn2��n��N*���������ʵ��t��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ��ԭ��Ϊ���㣬 ![]() ��������Ϊ���Ὠ��������ϵ����֪Բ
��������Ϊ���Ὠ��������ϵ����֪Բ![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ��ֱ��
��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ����������
����������![]() ��
��![]() ����
����![]() ����.
����.
������Բ![]() ��ֱ�����귽����
��ֱ�����귽����
������![]() ����
����![]() ��ֵ.
��ֵ.
���𰸡���1��![]() ����2��1.
����2��1.
�������������������1���ȸ���![]() ��Բ
��Բ![]() �ļ����귽�̻�Ϊֱ�����귽������2���Ƚ�ֱ�߲������̵�������
�ļ����귽�̻�Ϊֱ�����귽������2���Ƚ�ֱ�߲������̵�������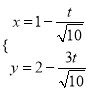 ���ٽ�ֱ�߲������̴���Բֱ�����귽�̣����ݲ������������
���ٽ�ֱ�߲������̴���Բֱ�����귽�̣����ݲ������������![]() ���������Τ�ﶨ�����
���������Τ�ﶨ�����
���������������![]() ����
����![]() ��
��
![]()
����![]() ��
�� ![]()
������ʽ��![]() ��
��
��![]() ����
����![]() ��
�� ![]() ��
��
![]()
![]()
![]() .
.
�����͡������
��������
23
����Ŀ��֤����������֪![]() ����ʵ������
����ʵ������![]() .��֤��
.��֤�� ![]() ��
��
������֪![]() ����
����![]() ��
�� ![]() ��
�� ![]() .��֤��
.��֤�� ![]() ��������һ���Ǹ���.
��������һ���Ǹ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����R�ϵ�ż�������ڣ���3����2����Ϊ�������Ҷ�x��R����f��2��x��=f��x������A��B�Ƕ۽�������ABC��������ǣ��� ��
A.f��sinA����f��cosB��
B.f��sinA����f��cosB��
C.f��sinA��=f��cosB��
D.f��sinA������f��cosB���Ĵ�С��ϵ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ ![]() ��������
�������� ![]() ������A��0����b����B��a��0����ֱ����ԭ��ľ���Ϊ
������A��0����b����B��a��0����ֱ����ԭ��ľ���Ϊ ![]() ��
��
��1������Բ�ķ��̣�
��2����֪����E����1��0������ֱ��y=kx+2��k��0������Բ����C��D���㣬�ʣ��Ƿ����k��ֵ��ʹ��CDΪֱ����Բ��E�㣿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���徭Ӫ�߰ѿ�ʼ����������A��B������Ʒ������Ͷ�������������г��±���
Ͷ��A��Ʒ����Ԫ�� | 1 | 2 | 3 | 4 | 5 | 6 |
��������Ԫ�� | 0.65 | 1.39 | 1.85 | 2 | 1.84 | 1.40 |
Ͷ��B��Ʒ����Ԫ�� | 1 | 2 | 3 | 4 | 5 | 6 |
��������Ԫ�� | 0.25 | 0.49 | 0.76 | 1 | 1.26 | 1.51 |
�þ�Ӫ��������Ͷ��12��Ԫ��Ӫ�����ֲ�Ʒ������֪Ͷ��A��B������Ʒ�����ٲ����������������ƶ�һ���ʽ�Ͷ�뷽����ʹ�øþ�Ӫ���ܻ�������������ķ�������þ�Ӫ�����¿ɻ�õ�������������������Ч���֣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ��Բ
��Բ![]() ��
��![]() ������һ�㣬��
������һ�㣬��![]() ���
���![]() ����ԭ��Գƣ��߶�
����ԭ��Գƣ��߶�![]() �Ĵ�ֱƽ������
�Ĵ�ֱƽ������![]() ����
����![]() ��.
��.
��1�����![]() �Ĺ켣
�Ĺ켣![]() �ķ��̣�
�ķ��̣�
��2������![]() �Ķ�ֱ��
�Ķ�ֱ��![]() ���
���![]() �Ĺ켣����
�Ĺ켣����![]() ���㣬��
���㣬��![]() �����Ƿ���ڶ���
�����Ƿ���ڶ���![]() ʹ��
ʹ��![]() Ϊֱ����Բ�������㣿�����ڣ������
Ϊֱ����Բ�������㣿�����ڣ������![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������������õ��Ϊ�߷�͵�����ʱ��ν��з�ʱ�Ƽۣ��õ����ĵ������۵�۱����£�
�߷�ʱ����õ�۸�� | ��ʱ����õ�۸�� | ||
�߷����� ����(�� λ��ǧ��ʱ) | �߷��� (��λ��Ԫ/ ǧ��ʱ) | ������ ����(��λ�� ǧ��ʱ) | �ȵ�� (��λ��Ԫ/ ǧ��ʱ) |
50������ �IJ��� | 0.568 | 50������ �IJ��� | 0.288 |
���� 50 �� 200 �IJ��� | 0.598 | ���� 50 �� 200 �IJ��� | 0.318 |
����200 �IJ��� | 0.668 | ���� 200 �IJ��� | 0.388 |
��ij��ͥ5�·ݵĸ߷�ʱ����õ���Ϊ 200 ǧ��ʱ����ʱ����õ���Ϊ 100 ǧ��ʱ�������ּƷѷ�ʽ�ü�ͥ����Ӧ���ĵ��Ϊ____________Ԫ��(����������)
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com