
| AΘ° | ΙιΡ…ΆΤάμΓΔ―ί“οΆΤάμ | BΘ° | άύ±»ΆΤάμΓΔ―ί“οΆΤάμ | ||
| CΘ° | ΙιΡ…ΆΤάμΓΔάύ±»ΆΤάμ | DΘ° | άύ±»ΆΤάμΓΔΙιΡ…ΆΤάμ |
Ζ÷Έω Θ®1Θ©ΗυΨίάύ±»ΒΡΖΫΖ®Θ§ΚΆάύ±»ΜΐΘ§Φ”άύ±»≥ΥΘ§”…¥Υάύ±»ΒΟ≥ωΫα¬έΘΜΘ®2Θ©”…ΧΊ βΒΫ“ΜΑψΒΡΆΤάμΘ§ «ΙιΡ…ΆΤάμΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ© «Β»≤ν ΐΝ–”κΒ»±» ΐΝ–Ϋα¬έΒΡάύ±»Θ§ τ”Ύάύ±»ΆΤάμΘΜ
Θ®2Θ©”…ΧΊ βΒΫ“ΜΑψΒΡΆΤάμΘ§ «ΙιΡ…ΆΤάμΘ§
Ι ―ΓDΘ°
ΒψΤά ±ΨΧβΩΦ≤ιΝΥάύ±»ΆΤάμΓΔΙιΡ…ΆΤάμΒΡΖΫΖ®ΚΆ”Π”ΟΈ ΧβΘ§ΫβΧβ ±”Π’ΤΈ’ΚΟάύ±»ΆΤάμΓΔΙιΡ…ΆΤάμΒΡΗ≈ΡνΘ§ «Μυ¥ΓΧβΘ°


 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 2$\sqrt{2}$ | BΘ° | $\sqrt{2}$ | CΘ° | $\frac{\sqrt{2}}{2}$ | DΘ° | 2 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 1 | BΘ° | $\sqrt{3}$ | CΘ° | 2 | DΘ° | 2$\sqrt{3}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
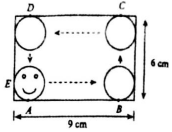 ”–“ΜΗωΒγΕ·ΆφΨΏΘ§Υϋ”–“ΜΗω9ΓΝ6ΒΡ≥ΛΖΫ–ΈΘ®ΒΞΈΜΘΚcmΘ©ΚΆ“ΜΗωΑκΨΕΈΣ1cmΒΡ–Γ‘≤≈ΧΘ®≈Χ÷–ΆόΆόΝ≥Θ©Θ§ΥϊΟ«ΒΡΝ§Ϋ”ΒψΈΣAΘ§EΘ§¥ρΩΣΒγ‘¥Θ§–Γ‘≤≈Χ―ΊΉ≈≥ΛΖΫ–ΈΡΎ±ΎΘ§¥”ΒψA≥ωΖΔ≤ΜΆΘΒΊΙωΕ·Θ®ΈόΜ§Ε·Θ©Θ§»γΆΦΥυ ΨΘ§»τ¥Υ ±Ρ≥»ΥœρΗΟ≥ΛΖΫ–Έ≈ΧΆΕ÷ά“ΜΟΕΖ…οΎΘ§‘ρΡή…δ÷––Γ‘≤≈Χ‘Υ––«χ”ρΡΎΒΡΗ≈¬ ΈΣ$\frac{40+Π–}{54}$Θ°
”–“ΜΗωΒγΕ·ΆφΨΏΘ§Υϋ”–“ΜΗω9ΓΝ6ΒΡ≥ΛΖΫ–ΈΘ®ΒΞΈΜΘΚcmΘ©ΚΆ“ΜΗωΑκΨΕΈΣ1cmΒΡ–Γ‘≤≈ΧΘ®≈Χ÷–ΆόΆόΝ≥Θ©Θ§ΥϊΟ«ΒΡΝ§Ϋ”ΒψΈΣAΘ§EΘ§¥ρΩΣΒγ‘¥Θ§–Γ‘≤≈Χ―ΊΉ≈≥ΛΖΫ–ΈΡΎ±ΎΘ§¥”ΒψA≥ωΖΔ≤ΜΆΘΒΊΙωΕ·Θ®ΈόΜ§Ε·Θ©Θ§»γΆΦΥυ ΨΘ§»τ¥Υ ±Ρ≥»ΥœρΗΟ≥ΛΖΫ–Έ≈ΧΆΕ÷ά“ΜΟΕΖ…οΎΘ§‘ρΡή…δ÷––Γ‘≤≈Χ‘Υ––«χ”ρΡΎΒΡΗ≈¬ ΈΣ$\frac{40+Π–}{54}$Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | kΘΦ1ΜρkΘΨ9 | BΘ° | 1ΘΦkΘΦ9 | CΘ° | 1ΘΦkΘΦ9«“kΓΌ5 | DΘ° | 5ΘΦkΘΦ9 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com