
 假定该产品产销平衡,根据上述统计规律求:
假定该产品产销平衡,根据上述统计规律求: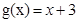 ,设利润函数为
,设利润函数为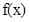 ,则
,则 ,
,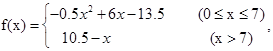 (1)要使工厂有盈利,则有f(x)>0,因为
(1)要使工厂有盈利,则有f(x)>0,因为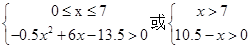 ,
,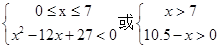 ⇒
⇒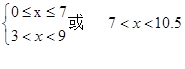
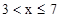 或
或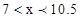 , 即
, 即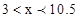 .
. 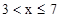 时,
时, 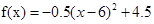
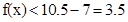 .
. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下:上市时间 天 天 | 4 | 10 | 36 |
市场价 元 元 | 90 | 51 | 90 |
 与上市时间
与上市时间 的变化关系并说明理由:①
的变化关系并说明理由:①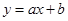 ;②
;② ;③
;③ .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. 小时 小时 | B. 小时 小时 | C.5小时 | D.10小时 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(-∞,2) | B.(4,+∞) |
| C.(-∞,2)∪(4,+∞) | D.(2,4) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 =C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )
=C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )A. | B.2 |
| C.4 | D.2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com