
分析 (1)结合充要条件的定义,作出集合A,B的图象,利用(A∪B)∩C为两个元素的集合,说明①直线ax+y=1和x+ay=1与圆x2+y2=1各有一个交点且不重合,②直线ax+y=1和x+ay=1重合,且与圆x2+y2=1有两个不同的交点,求实数a即可;
(2)结合充要条件的定义,若(A∪B)∩C为含三个元素的集合,a≠0,a≠1.直线ax+y=1和x+ay=1与圆x2+y2=1必须交于三个点,即两直线有一个交点在圆x2+y2=1上,且两直线与圆还各有一个交点,利用对称性求出实数a即可.
解答 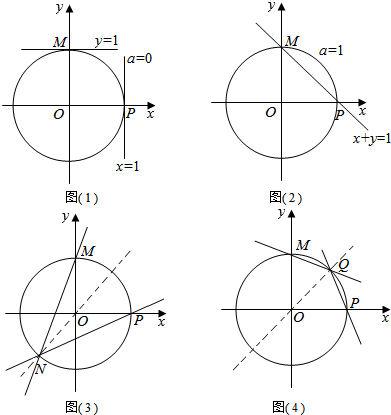 解:(1)若(A∪B)∩C含两个元素
解:(1)若(A∪B)∩C含两个元素
①直线ax+y=1和x+ay=1与圆x2+y2=1各有一个交点且不重合,则满足条件,此时a=0,如图(1)所示
②直线ax+y=1和x+ay=1重合,且与圆x2+y2=1有两个不同的交点,则满足条件,此时a=1,如图(2)所示
综上,a=0或a=1时,(A∪B)∩C为含两个元素的集合,
反之也成立,
即(A∪B)∩C的元素个数为2的充要条件是a=0或a=1.
(2)(A∪B)∩C含三个元素
显然a≠0,a≠1.
直线ax+y=1和x+ay=1与圆x2+y2=1必须交于三个点,即两直线有一个交点在圆x2+y2=1上,且两直线与圆还各有一个交点
∵直线ax+y=1和x+ay=1关于直线y=x对称
∴三个交点为(0,1),(1,0),($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)或(0,1),(1,0),(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$)
如图(3)(4)所示
此时a=-1±$\sqrt{2}$.
反之也成立,
即(A∪B)∩C的元素个数为3的充要条件是a=-1±$\sqrt{2}$.
点评 本题考查充要条件的求解,子集、并集、交集的转换,考查数形结合,分类讨论的思想,转化思想的应用,作出图形,是解好本题的前提,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 已知如图所示,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
已知如图所示,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [12,24] | B. | [8,12] | C. | [8,24] | D. | [8,17] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=N,B=N+,f:x→|x-1| | |
| B. | A={中国人民银行发行的储蓄卡},B={所有的4位数},f:取储蓄卡号后4位 | |
| C. | A={开国十大元帅},B=R,f:取出生年份 | |
| D. | A=R,B={1},f:x→1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 15 | C. | 5 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com