
某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
| | 喜欢 | 不喜欢 | 合计 |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
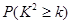 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
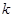 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
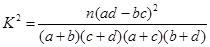 ,其中
,其中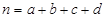 )
) (1)有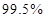 的把握认为喜欢“人文景观”景点与年龄有关;(2)
的把握认为喜欢“人文景观”景点与年龄有关;(2)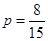 .
.
解析试题分析:本题主要考查独立性检验、分层抽样、随机事件的概率等基础知识,同时考查分析数据的能力、分析问题解决问题的能力和计算求解能力.第一问,由已知表格读出a,b,c,d,n,利用已知的公式先求出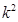 的值,与临界值表进行对比,找到相关的概率值;第二问,利用分层抽样的公式“样本容量÷总容量”求出大于40岁和20岁至40岁所抽取的人数,并用字母表示,写出在6人中选2人的所以情况,在其中找出符合题意的情况,用这2个种数求概率.
的值,与临界值表进行对比,找到相关的概率值;第二问,利用分层抽样的公式“样本容量÷总容量”求出大于40岁和20岁至40岁所抽取的人数,并用字母表示,写出在6人中选2人的所以情况,在其中找出符合题意的情况,用这2个种数求概率.
试题解析:(1)由公式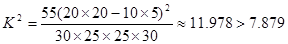
所以有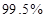 的把握认为喜欢“人文景观”景点与年龄有关 5分
的把握认为喜欢“人文景观”景点与年龄有关 5分
(2)设所抽样本中有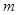 个“大于40岁”市民,则
个“大于40岁”市民,则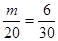 ,得
,得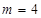 人
人
所以样本中有4个“大于40岁”的市民,2个“20岁至40岁”的市民,分别记作 ,从中任选2人的基本事件有
,从中任选2人的基本事件有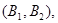
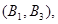

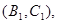
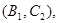
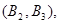

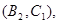
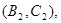
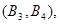
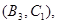
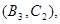
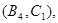
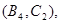
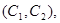 共15个 9分
共15个 9分
其中恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的事件有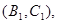
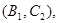
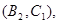
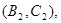
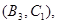
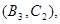
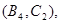 共8个
共8个
所以恰有1名“大于40岁”和1名“20岁至40岁”之间的市民的概率为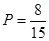 12分
12分
考点:1.分层抽样;2.独立性检验.


科目:高中数学 来源: 题型:解答题
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取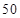 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为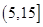 ,
,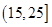 ,
,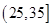 ,
, ,由此得到样本的重量频率分布直方图,如图
,由此得到样本的重量频率分布直方图,如图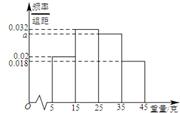
(1)求 的值;
的值;
(2)根据样本数据,试估计盒子中小球重量的平均值;
(注:设样本数据第 组的频率为
组的频率为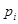 ,第
,第 组区间的中点值为
组区间的中点值为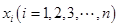 ,则样本数据的平均值为
,则样本数据的平均值为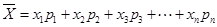 .)
.)
(3)从盒子中随机抽取 个小球,其中重量在
个小球,其中重量在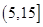 内的小球个数为
内的小球个数为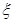 ,求
,求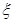 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某化肥厂有甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量(单位:kg),分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种方法?
(2)试计算甲、乙车间产品重量的平均数与方差,并说明哪个车间产品较稳定?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如下.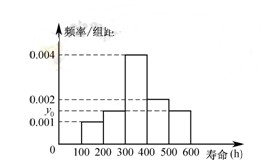
(1)求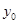 ,并根据图中的数据,用分层抽样的方法抽取
,并根据图中的数据,用分层抽样的方法抽取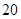 个元件,元件寿命落在
个元件,元件寿命落在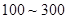 之间的应抽取几个?
之间的应抽取几个?
(2)从(1)中抽出的寿命落在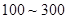 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个元件寿命落在
个元件,求事件“恰好有一个元件寿命落在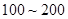 之间,一个元件寿命落在
之间,一个元件寿命落在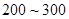 之间”的概率.
之间”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位: )
)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在上面给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
| API | 0~50 | 51~ 100 | 101~ 150 | 151~ 200 | 201~ 250 | 251~ 300 | >300 |
| 级 别 | Ⅰ | Ⅱ | Ⅲ1 | Ⅲ2 | Ⅳ1 | Ⅳ2 | Ⅴ |
| 状 况 | 优 | 良 | 轻微 污染 | 轻度 污染 | 中度 污染 | 中度 重污染 | 重度 污染 |
| |  |  |  |  |  | ||

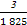 +
+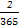 +
+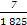 +
+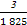 +
+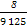 =
=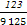 ,365=73×5).
,365=73×5).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设三组实验数据(x1,y1),(x2,y2),(x3,y3)的回归直线方程是: =
= x+
x+ ,使代数式[y1-(
,使代数式[y1-( x1+
x1+ )]2+[y2-(
)]2+[y2-( x2+
x2+ )]2+[y3-(
)]2+[y3-( x3+
x3+ )]2的值最小时,
)]2的值最小时, =
= -
-
 ,
, =
=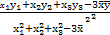 (
( ,
, 分别是这三组数据的横、纵坐标的平均数),
分别是这三组数据的横、纵坐标的平均数),
若有7组数据列表如下:
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
 xi+
xi+ )|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.
)|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,
8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段,从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制直方图如图所示.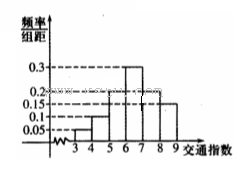
(1)这20个路段轻度拥堵、中度拥堵的路段各有多少个?
(2)从这20个路段中随机抽出的3个路段,用X表示抽取的中度拥堵的路段的个数,求X的分布列及期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com