
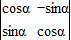 对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵;
对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵; .
.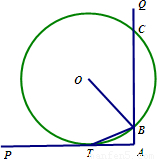
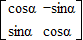 对应变换的作用下得到的点为B(-2,2),建立方程,求得M,再利用
对应变换的作用下得到的点为B(-2,2),建立方程,求得M,再利用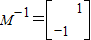 ,可得矩阵M的逆矩阵,或利用矩阵M的行列式,求得矩阵M的逆矩阵;
,可得矩阵M的逆矩阵,或利用矩阵M的行列式,求得矩阵M的逆矩阵; ,即可求AB的最小值;
,即可求AB的最小值;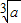 ,同理,2aj≥1+1+aj≥3
,同理,2aj≥1+1+aj≥3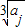 ,将上述不等式两边相乘,利用a1•a2•…•an=1,即可证得结论.
,将上述不等式两边相乘,利用a1•a2•…•an=1,即可证得结论.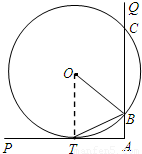 (1)证明:连接OT,因为AT是切线,所以OT⊥AP.
(1)证明:连接OT,因为AT是切线,所以OT⊥AP.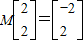 ,即
,即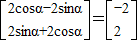 ,
,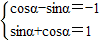 ,解得
,解得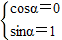
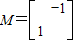 .(5分)
.(5分)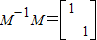 ,解得
,解得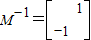 .(10分)
.(10分)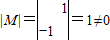 ,所以
,所以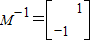 .
.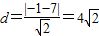 ,所以(AB)min=
,所以(AB)min=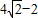 . (10分)
. (10分) ,(5分)
,(5分)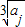 ,
,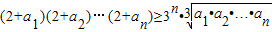 ,
,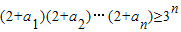 .(10分)
.(10分)

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
 (1)如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA
(1)如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (几何证明选做题)如图,∠PAQ是直角,半径为5的圆O与AP相切于点T,与AQ相交于两点B、C,BT是否平分∠OBA?证明你的结论;
(几何证明选做题)如图,∠PAQ是直角,半径为5的圆O与AP相切于点T,与AQ相交于两点B、C,BT是否平分∠OBA?证明你的结论;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com