
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
我们把定义在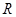 上,且满足
上,且满足 (其中常数
(其中常数 满足
满足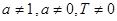 )的函数叫做似周期函数.
)的函数叫做似周期函数.
(1)若某个似周期函数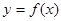 满足
满足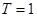 且图像关于直线
且图像关于直线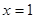 对称.求证:函数
对称.求证:函数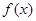 是偶函数;
是偶函数;
(2)当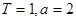 时,某个似周期函数在
时,某个似周期函数在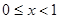 时的解析式为
时的解析式为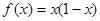 ,求函数
,求函数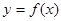 ,
,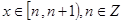 的解析式;
的解析式;
(3)对于确定的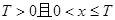 时,
时,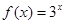 ,试研究似周期函数函数
,试研究似周期函数函数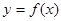 在区间
在区间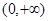 上是否可能是单调函数?若可能,求出
上是否可能是单调函数?若可能,求出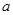 的取值范围;若不可能,请说明理由.
的取值范围;若不可能,请说明理由.
(1)因为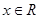 关于原点对称, 又函数
关于原点对称, 又函数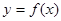 的图像关于直线
的图像关于直线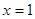 对称,所以
对称,所以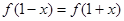 又
又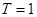 ,
,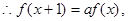 用
用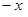 代替
代替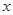 得
得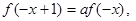 可知
可知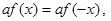
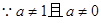 ,
,
 .即函数
.即函数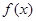 是偶函数;(2)
是偶函数;(2)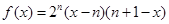 ;(3)
;(3)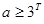 .
.
【解析】
试题分析:因为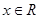 关于原点对称, 又函数
关于原点对称, 又函数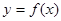 的图像关于直线
的图像关于直线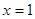 对称,
对称,
所以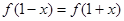 , 又
, 又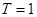 ,
,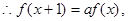 用
用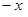 代替
代替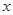 得
得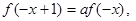 可知
可知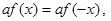
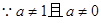 ,
,
 .即函数
.即函数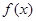 是偶函数;
是偶函数;
(2)当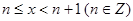 时,
时,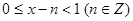
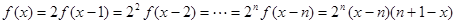 ;
;
(3)当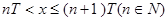 时,
时,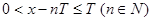
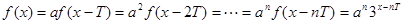
显然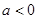 时,函数
时,函数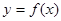 在区间
在区间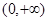 上不是单调函数
上不是单调函数
又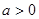 时,
时,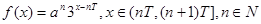 是增函数,
是增函数,
此时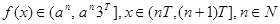
若函数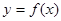 在区间
在区间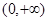 上是单调函数,那么它必须是增函数,则必有
上是单调函数,那么它必须是增函数,则必有
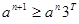 ,解得
,解得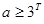 .
.
考点:本题考查了函数的性质
点评:函数的基本性质有单调性和奇偶性,它们是函数的两个重要的性质,在解决函数问题中起着非常重要的作用,主要用于判断函数单调性、求最值、求参数的取值范围等


科目:高中数学 来源: 题型:
(本题满分18分,第(1)小题6分,第(2)小题6分,第(3)小题6分)
若数列![]() 满足:
满足:![]() 是常数),则称数列
是常数),则称数列![]() 为二阶线性递推数列,且定义方程
为二阶线性递推数列,且定义方程![]() 为数列
为数列![]() 的特征方程,方程的根称为特征根; 数列
的特征方程,方程的根称为特征根; 数列![]() 的通项公式
的通项公式![]() 均可用特征根求得:
均可用特征根求得:
①若方程![]() 有两相异实根
有两相异实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
②若方程![]() 有两相同实根
有两相同实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
再利用![]() 可求得
可求得![]() ,进而求得
,进而求得![]() .
.
根据上述结论求下列问题:
(1)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(2)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(3)当![]() ,
,![]() (
(![]() )时,记
)时,记![]() ,若
,若![]() 能被数
能被数![]() 整除,求所有满足条件的正整数
整除,求所有满足条件的正整数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源:2011届上海市卢湾区高三上学期期末数学理卷 题型:解答题
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分.
已知负数 和正数
和正数 ,且对任意的正整数n,当
,且对任意的正整数n,当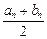 ≥0时, 有[
≥0时, 有[ ,
,  ]=
]=
[ ,
, 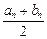 ];当
];当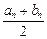 <0时, 有[
<0时, 有[ ,
,  ]= [
]= [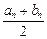 ,
, 
 ].
].
(1)求证数列{ }是等比数列;
}是等比数列;
(2)若 ,求证
,求证
 ;
;
(3)是否存在 ,使得数列
,使得数列 为常数数列?请说明理由
为常数数列?请说明理由
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济宁市高三第二次月考文科数学 题型:解答题
(本题满分18分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
(Ⅲ)过A、B分别作抛物C的切线 且
且 交于点M,求
交于点M,求 与
与 面积之和的最小值.
面积之和的最小值.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市青浦区高三上学期期终学习质量调研测试数学试卷 题型:解答题
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设 ,对于项数为
,对于项数为 的有穷数列
的有穷数列 ,令
,令 为
为 中最大值,称数列
中最大值,称数列 为
为 的“创新数列”.例如数列
的“创新数列”.例如数列 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7.
考查自然数 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
.
(1)若 ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列 ;
;
(2)是否存在数列 的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
(3)是否存在数列 ,使它的创新数列为等差数列?若存在,求出满足所有条件的数列
,使它的创新数列为等差数列?若存在,求出满足所有条件的数列 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:上海市普陀区2010届高三第二次模拟考试数学文 题型:解答题
(本题满分18分,其中第1小题6分,第2小题6分,第3小题6分)
已知数列 的首项为1,前
的首项为1,前 项和为
项和为 ,且满足
,且满足 ,
, .数列
.数列 满足
满足 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 当 时,试比较
时,试比较 与
与 的大小,并说明理由;
的大小,并说明理由;
(3) 试判断:当 时,向量
时,向量
 是否可能恰为直线
是否可能恰为直线
 的方向向量?请说明你的理由.
的方向向量?请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com