
【题目】已知函数f(x)的图象是由函数![]() 的图象经如下变换得到:先将g(x)图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图象向右平移
的图象经如下变换得到:先将g(x)图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图象向右平移![]() 个单位长度.
个单位长度.
(1)求函数f(x)的解析式,并求其图象的对称轴方程;
(2)已知关于x的方程f(x)+g(x)=m在![]() 内有两个不同的解
内有两个不同的解![]() .
.
①求实数m的取值范围;
②证明:![]() .
.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是________.(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加夏令营的400名学生编号为:001,002,…,400,采用系统抽样的方法抽取一个容量为40的样本,且随机抽得的号码为003,这400名学生分住在三个营区,从001到180在第一营区,从181到295在第二营区,从296到400在第三营区,三个营区被抽中的人数分别为( )
A. 18,12,10 B. 20,12,8 C. 17,13,10 D. 18,11,11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x与椭圆E:![]() 1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|
1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|![]() .
.
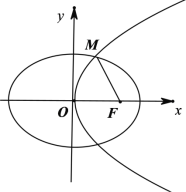
(1)求椭圆E的标准方程;
(2)过点P(1,![]() )的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
)的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过右焦点
,过右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,点
,点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 、
、![]() 的斜率
的斜率![]() ,
,![]() ,请问
,请问![]() 是否为定值?若是定值,求出其定值;若不是,说明理由.
是否为定值?若是定值,求出其定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为3的正![]() 的各边三等分,过每个分点分别作另外两边的平行线,称
的各边三等分,过每个分点分别作另外两边的平行线,称![]() 的边及这些平行线所交的10个点为格点.若在这10个格点中任取
的边及这些平行线所交的10个点为格点.若在这10个格点中任取![]() 个格点,一定存在三个格点能构成一个等腰三角形(包括正三角形).求
个格点,一定存在三个格点能构成一个等腰三角形(包括正三角形).求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com