
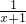 ;
;  的图象向左平移一个单位
的图象向左平移一个单位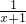 的图象
的图象 的定义域为{x|x≠0},值域为{y|y≠0},
的定义域为{x|x≠0},值域为{y|y≠0},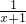 的定义域为{x|x≠-1},值域为{y|y≠0},
的定义域为{x|x≠-1},值域为{y|y≠0},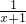 的图象是由函数y=
的图象是由函数y= 的图象向左平移一个单位得到的,由反比例函数的图象和性质,可得函数的定义域和值域;
的图象向左平移一个单位得到的,由反比例函数的图象和性质,可得函数的定义域和值域;

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com