将大小相同5个不同颜色的小球,放在A、B、C、D、E共5个盒子中,每个球可以任意放在一个盒子里,则恰有两个盒子空且A盒子最多放1个球的放球方法总数为 .
【答案】
分析:①若A盒为空:则从剩余的4个盒子中选出3个盒子,使各个盒子中的小球数为3、1、1求得方法数;若3个盒子中小球的数量为2、2、1,求得方法数,相加即得此时方法数为600.
②若A盒不为空(即放一个球)求得方法数为420,再把①②的方法数相加,即得所求.
解答:解:①若A盒为空:这相当于5个球进入了3个盒子中.
则从剩余的4个盒子中选出3个盒子,使各个盒子中的小球数为3、1、1,方法有
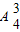
•
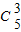
=240种,
若3个盒子中小球的数量为2、2、1,则有(
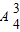
•
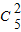
•

•

)÷

=360种,
故此时方法共有240+360=600种.
②若A盒不为空(即放一个球)则先把A盒子中放入一个球,方法有5种,
再从剩余的4个盒子中取出2个盒子,放入小球,方法有5

(

+

)=420种.
综上,放球的方法有600+420=1020种,
故答案为 1020.
点评:本题主要考查排列与组合及两个基本原理的应用,属于中档题.

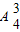 •
•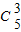 =240种,
=240种,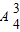 •
•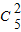 •
• •
• )÷
)÷ =360种,
=360种, (
(  +
+ )=420种.
)=420种.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案