
分析 (1)g(x)-f(x)>x2+x+e-ex等价于ex+lnx-e>0,令h(x)=ex+lnx-e,则$h'(x)={e^x}+\frac{1}{x}>0$,可知函数h(x)在(1,+∞)上单调递增,即可证明结论;
(2)不等式2f(x)>3x2+a等价于(2x2-4ax)lnx+x2-a>0,构造函数,先求出a的范围,再验证即可.
解答 (1)证明:当a=1,b=-1时,f(x)=(x2-2x)lnx-x2,
所以g(x)-f(x)>x2+x+e-ex等价于ex+lnx-e>0,
令h(x)=ex+lnx-e,则$h'(x)={e^x}+\frac{1}{x}>0$,可知函数h(x)在(1,+∞)上单调递增,
所以h(x)>h(1),即ex+lnx>e,亦即ex+lnx-e>0;
(2)解:当b=2时,f(x)=(x2-2ax) lnx+2x2,a∈R,
所以不等式2f(x)>3x2+a等价于(2x2-4ax)lnx+x2-a>0,
令p(x)=(2x2-4ax)lnx+x2-a,x∈[1,+∞),
则p(x)=(2x2-4ax)lnx+x2-a>0在[1,+∞)上恒成立,所以p(1)=1-a>0,所以a<1,
又p(x)=(4x-4a)lnx+(2x-4a)+2x=4(x-a)(lnx+1)(x≥1),
显然当a<1时,p(x)>0,则函数p(x)在[1,+∞)上单调递增,
所以p(x)min=p(1)=1-a>0,所以a<1,
综上可知a的取值范围为(-∞,1).
点评 本题考查了导数知识的综合运用,考查函数的最值的问题,以及参数的取值范围,属于中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
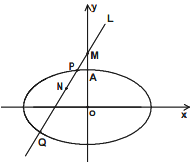 如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于不同两点P,Q,点N在线段PQ上.
如图,已知椭圆的中心在坐标原点,焦点在x轴上,它的一个顶点为A(0,$\sqrt{2}$),且离心率等于$\frac{{\sqrt{3}}}{2}$,过点M(0,2)的直线l与椭圆相交于不同两点P,Q,点N在线段PQ上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
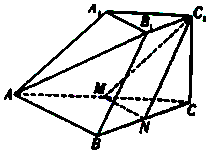 如图,在三棱台ABC-A1B1C1中,CC1⊥平面ABC,AB=2A1B1=2CC1,M,N分别为AC,BC的中点.
如图,在三棱台ABC-A1B1C1中,CC1⊥平面ABC,AB=2A1B1=2CC1,M,N分别为AC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (0,$\frac{1}{2}$)∪(2,+∞) | C. | (0,$\frac{1}{8}$)∪($\frac{1}{2}$,2) | D. | (0,$\frac{1}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com