
【题目】已知函数f(x)=x3+3x2-9x .
(I)求f(x)的单调区间;
(Ⅱ)若函数f(x)在区间[-4,c]上的最小值为-5,求c的取值范围.
【答案】解:(I)f(x)=x3+3x2-9x的定义域是R,且f '(x)=3x2+6x-9 =3(x+3)(x-1)
令f '(x)=0,得x1=-3,x2=1,
f(x)与f '(x)在(- ![]() ,+
,+ ![]() )上的情况如下:
)上的情况如下:
x | (+ | -3 | (-3,1) | 1 | (1,+ |
f '(x) | + | 0 | - | 0 | + |
f(x) | ↗ | 27 | ↘ | -5 | ↗ |
所以f(x)的单调递增区间为(- ![]() ,-3)和(1,+
,-3)和(1,+ ![]() );单调递减区间为(-3,1),
);单调递减区间为(-3,1),
(II)由f(-4)=-64+48+36=20及(I)中结论可知:
当c≥1时,函数f(x)在区间[-4,c]上的最小值为f(1)=1+3-9 =-5;
当-4<c<1时,函数f(x)在区间[-4,c]上的最小值大于-5,不合题意舍,
因此,c的取值范围是[1,+ ![]() ).
).
【解析】(1)求出函数的导函数,解关于导函数的不等式,即可求出函数的单调区间。(2)通过讨论c的范围,求出函数的最值从而求出c的取值范围。
【考点精析】掌握二次函数在闭区间上的最值和利用导数研究函数的单调性是解答本题的根本,需要知道当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() ;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间
;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点P(0,1)在圆C:x2+y2+2mx﹣2y+m2﹣4m+1=0内,若存在过点P的直线交圆C于A、B两点,且△PBC的面积是△PAC的面积的2倍,则实数m的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一系列对应值如下表:
的一系列对应值如下表:

(1)根据表格提供的数据求出函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数![]() 的周期为
的周期为![]() ,当
,当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣k(
﹣k( ![]() +lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
+lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
A.(﹣∞,e]
B.[0,e]
C.(﹣∞,e)
D.[0,e)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2017年1月18日开始,支付宝用户可以通过“![]() 扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜
扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜![]() ,每一位提前集齐五福的用户都将获得一份现金红包.某髙校一个社团在年后开学后随机调査了80位该校在读大学生,就除夕夜
,每一位提前集齐五福的用户都将获得一份现金红包.某髙校一个社团在年后开学后随机调査了80位该校在读大学生,就除夕夜![]() 之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
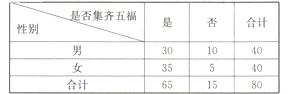
(1)计算这80位大学生集齐五福的频率,并据此估算该校10000名在读大学生中集齐五福的人数;
(2)为了解集齐五福的大学生明年是否愿意继续参加集五福活动,该大学的学生会从集齐五福的学生中,选取2位男生和3位女生逐个进行采访,最后再随机选取3次采访记录放到该大学的官方网站上,求最后被选取的3次采访对象中至少有一位男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2eax .
(Ⅰ)当a<0时,讨论函数f(x)的单调性;
(Ⅱ)在(1)条件下,求函数f(x)在区间[0,1]上的最大值;
(Ⅲ)设函数g(x)=2ex﹣ ![]() ,求证:当a=1,对x∈(0,1),g(x)﹣xf(x)>2恒成立.
,求证:当a=1,对x∈(0,1),g(x)﹣xf(x)>2恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD与AB垂直,并与AB相交于点E,点F为弦CD上异于点E的任意一点,连接BF、AF并延长交⊙O于点M、N. 
(1)求证:B、E、F、N四点共圆;
(2)求证:AC2+BFBM=AB2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com