
【题目】设函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题(1)利用![]() ,化简函数求出切点坐标,求解是的导数,得到切线方程的斜率,即可求解切线方程.(2)求出函数的导数,利用导数为
,化简函数求出切点坐标,求解是的导数,得到切线方程的斜率,即可求解切线方程.(2)求出函数的导数,利用导数为![]() ,得到极值点,然后①当
,得到极值点,然后①当![]() 时,②当
时,②当![]() ,③当
,③当![]() ,④当
,④当![]() ,⑤当
,⑤当![]() ,分别求解函数的单调性推出最值,解得
,分别求解函数的单调性推出最值,解得![]() 的取值范围.第(2)问另解:
的取值范围.第(2)问另解:![]() 当
当![]() 时的最大值为
时的最大值为![]() ,等价于
,等价于![]() 对于
对于![]() 恒成立,转化
恒成立,转化![]() 的函数,构造新函数,利用增函数的导数求解最值即可.
的函数,构造新函数,利用增函数的导数求解最值即可.
试题解析:(1)当![]() 时,
时,![]()
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
(2)![]()
令![]() 得
得![]()
①当![]() 时,
时,![]() 在
在![]() 递减,在
递减,在![]() 递增
递增
当![]() ,
,![]()
②当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 递减,在
递减,在![]() 递增
递增
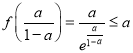 解得
解得![]() 所以
所以![]()
③当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 递减,
递减,![]()
④当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 递减,在
递减,在![]() 递增
递增
![]() 解得
解得![]() 所以
所以![]()
⑤当![]() 即
即![]() 时,
时,![]() 在
在![]() 递增,
递增,![]() 不合题意
不合题意
综上所述:![]() 的取值范围为
的取值范围为![]()
第(2)问另解:![]()
![]() 当
当![]() 时的最大值为
时的最大值为![]() ,等价于
,等价于![]() 对于
对于![]() 恒成立
恒成立
可化为![]() 对于
对于![]() 恒成立
恒成立
令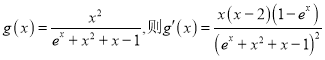
于是![]() 在
在![]() 递增,在
递增,在![]() 递减
递减
![]()
![]() 的取值范围为
的取值范围为![]()


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】设点![]() 为椭圆
为椭圆![]() 的左焦点,直线
的左焦点,直线![]() 被椭圆
被椭圆![]() 截得弦长为
截得弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆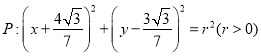 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 为线段
为线段![]() 上任意一点,直线
上任意一点,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点
两点![]() 为圆
为圆![]() 的直径,且直线
的直径,且直线![]() 的斜率大于
的斜率大于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在矩形![]() 中,
中,![]() ,沿直线BD将△ABD折成
,沿直线BD将△ABD折成![]() ,使得点
,使得点![]() 在平面
在平面![]() 上的射影在
上的射影在![]() 内(不含边界),设二面角
内(不含边界),设二面角![]() 的大小为
的大小为![]() ,直线
,直线![]() ,
,![]() 与平面
与平面![]() 中所成的角分别为
中所成的角分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件。从某企业生产的桥梁构件中抽取![]() 件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
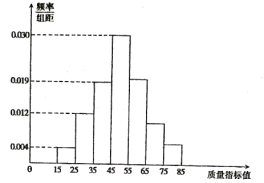
(1)求这些桥梁构件质量指标值落在区间![]() 内的频率;
内的频率;
(2)用分层抽样的方法在区间![]() 内抽取一个容量为
内抽取一个容量为![]() 的样本,将该样本看成一个总体,从中任意抽取
的样本,将该样本看成一个总体,从中任意抽取![]() 件桥梁构件,求这
件桥梁构件,求这![]() 件桥梁构件都在区间
件桥梁构件都在区间![]() 内的概率
内的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:![]() .
.
(1)求圆的圆心C的坐标和半径长;
(2)直线l经过坐标原点且不与y轴重合,l与圆C相交于![]() 两点,求证:
两点,求证:![]() 为定值;
为定值;
(3)斜率为1的直线m与圆C相交于D、E两点,求直线m的方程,使![]() 的面积最大.
的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() .
.
(1)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
(2)过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,设
两点,设![]() 为原点.
为原点.
(ⅰ)当直线![]() 的斜率为1时,求
的斜率为1时,求![]() 的面积;
的面积;
(ⅱ)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蛋糕店每天做若干个生日蛋糕,每个制作成本为50元,当天以每个100元售出,若当天白天售不出,则当晚以30元/个价格作普通蛋糕低价售出,可以全部售完.
(1)若蛋糕店每天做20个生日蛋糕,求当天的利润![]() (单位:元)关于当天生日蛋糕的需求量
(单位:元)关于当天生日蛋糕的需求量![]() (单位:个,
(单位:个, ![]() )的函数关系;
)的函数关系;
(2)蛋糕店记录了100天生日蛋糕的日需求量(单位:个)整理得下表:

(ⅰ)假设蛋糕店在这100天内每天制作20个生日蛋糕,求这100天的日利润(单位:元)的平均数;
(ⅱ)若蛋糕店一天制作20个生日蛋糕,以100天记录的各需求量的频率作为概率,求当天利润不少于900元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:

其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,![]() 代表“生活不能自理”,按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位,则被访问地3位老龄人中恰有1位老龄人的健康指数不大于0的概率为___
代表“生活不能自理”,按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位,则被访问地3位老龄人中恰有1位老龄人的健康指数不大于0的概率为___
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com