
 个家庭的月收入
个家庭的月收入 (单位:千元)与月储蓄
(单位:千元)与月储蓄 (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得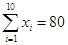 ,
, ,
, ,
, .
. 对月收入
对月收入 的线性回归方程
的线性回归方程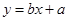 ;
; 与
与 之间是正相关还是负相关;
之间是正相关还是负相关; ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为
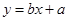 中,
中, ,
, ,
, 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
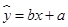 近似的刻画其相关关系,根据图形,以下结论最有可能成立的是( )
近似的刻画其相关关系,根据图形,以下结论最有可能成立的是( )
| A.线性相关关系较强,b的值为1.25 |
| B.线性相关关系较强,b的值为O.83 |
| C.线性相关关系较强,b的值为-0.87 |
| D.线性相关关系太弱,无研究价值 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
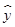 =3x+20,若
=3x+20,若 =18,则
=18,则 =________.
=________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 以上的把握认为这个结论是成立的。下列说法中正确的是( )
以上的把握认为这个结论是成立的。下列说法中正确的是( )| A.100个心脏病患者中至少有99人打酣 |
| B.1个人患心脏病,那么这个人有99%的概率打酣 |
| C.在100个心脏病患者中一定有打酣的人 |
| D.在100个心脏病患者中可能一个打酣的人都没有 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ≈5.059)
≈5.059)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,其中
,其中 .
.| K2≥k0 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 )的四组数值分别是
)的四组数值分别是 | 1 | 2 | 3 | 4 |
 | 3 | 3.8 | 5.2 | 6 |
 ,据此模型预报当
,据此模型预报当 为5时,
为5时, 的值为( )
的值为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com