
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若对于定义域内任意的![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)记![]() ,若
,若![]() 在区间
在区间![]() 内有两个零点,求
内有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递减(2)
上单调递减(2)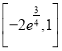 (3)
(3)![]()
【解析】
(1)代入求导分析定义内导数的正负以及原函数的单调性即可.
(2)求导函数的零点可得![]() 再分
再分![]() ,
,![]() 与
与![]() 三种情况得出函数的单调性进而求得
三种情况得出函数的单调性进而求得![]() 的最大值与
的最大值与![]() 的取值范围即可.
的取值范围即可.
(3)参变分离得![]() ,再分析
,再分析![]() 的单调性与值域,从而求得
的单调性与值域,从而求得![]() 的取值范围.或直接根据
的取值范围.或直接根据![]() 求导分
求导分![]() 与
与![]() 和
和![]() 三种情况讨论,利用零点存在定理列式求解即可.
三种情况讨论,利用零点存在定理列式求解即可.
(1)当![]() 时,
时, ![]() ,
,
![]() 的定义域为
的定义域为![]() ,
,![]()
令![]() 得
得![]() (舍负)
(舍负)
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递减.
上单调递减.
(2)![]() .
.
令![]() 有
有![]()
当![]() 时,
时,![]() 恒成立;
恒成立;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增
上单调递增
![]() ,
,![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增
上单调递增
![]() ,
,![]() ;
;
综上: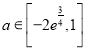
(3)法一:显然,![]() 不是
不是![]() 的零点∴
的零点∴![]()
由![]() 得
得![]() (*)
(*)
![]() ,令
,令![]() 得
得![]()
![]() 在
在![]() 和
和![]() 单调递减,
单调递减,![]() 单调递增
单调递增
又![]() 时,
时,![]() ,(*)不成立
,(*)不成立
所以只需 ,
,
故![]()
法二:![]() ,
,![]()
当![]() 时,不合题意,舍去;
时,不合题意,舍去;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
要使![]() 在区间
在区间![]() 内有两个零点,则需满足
内有两个零点,则需满足
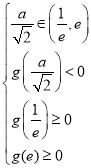 ,得到
,得到![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,
要使![]() 在区间
在区间![]() 内有两个零点,则需满足
内有两个零点,则需满足
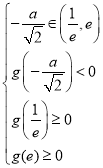 ,得到
,得到![]() ;
;
综上:![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】地球上的风能取之不尽,用之不竭.风能是淸洁能源,也是可再生能源.世界各国致力于发展风力发电,近10年来,全球风力发电累计装机容量连年攀升,中国更是发展迅猛,2014年累计装机容量就突破了![]() ,达到
,达到![]() ,中国的风力发电技术也日臻成熟,在全球范围的能源升级换代行动中体现出大国的担当与决心.以下是近10年全球风力发电累计装机容量与中国新增装机容量图. 根据所给信息,正确的统计结论是( )
,中国的风力发电技术也日臻成熟,在全球范围的能源升级换代行动中体现出大国的担当与决心.以下是近10年全球风力发电累计装机容量与中国新增装机容量图. 根据所给信息,正确的统计结论是( )
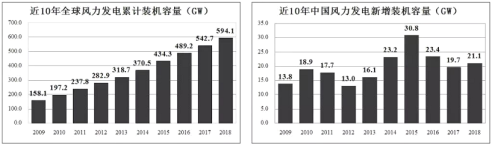
A.截止到2015年中国累计装机容量达到峰值
B.10年来全球新增装机容量连年攀升
C.10年来中国新增装机容量平均超过![]()
D.截止到2015年中国累计装机容量在全球累计装机容量中占比超过![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 的图像是一条连续不断的曲线,且在任意区间上
的图像是一条连续不断的曲线,且在任意区间上![]() 都不是常值函数.设
都不是常值函数.设![]() ,其中分点
,其中分点![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间
个小区间![]() ,记
,记![]() ,称为
,称为![]() 关于区间
关于区间![]() 的
的![]() 阶划分“落差总和”.
阶划分“落差总和”.
当![]() 取得最大值且
取得最大值且![]() 取得最小值
取得最小值![]() 时,称
时,称![]() 存在“最佳划分”
存在“最佳划分”![]() .
.
(1)已知![]() ,求
,求![]() 的最大值
的最大值![]() ;
;
(2)已知![]() ,求证:
,求证:![]() 在
在![]() 上存在“最佳划分”
上存在“最佳划分”![]() 的充要条件是
的充要条件是![]() 在
在![]() 上单调递增.
上单调递增.
(3)若![]() 是偶函数且存在“最佳划分”
是偶函数且存在“最佳划分”![]() ,求证:
,求证:![]() 是偶数,且
是偶数,且![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P到直线![]() 的距离与到点
的距离与到点![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点P的轨迹![]() ;
;
(2)直线![]() 与曲线
与曲线![]() 交于不同的两点A,B(A,B在
交于不同的两点A,B(A,B在![]() 轴的上方)
轴的上方)![]() :
:
①当A为椭圆与![]() 轴的正半轴的交点时,求直线
轴的正半轴的交点时,求直线![]() 的方程;
的方程;
②对于动直线![]() ,是否存在一个定点,无论
,是否存在一个定点,无论![]() 如何变化,直线
如何变化,直线![]() 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 ,(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为(ρ﹣2cosθ)2=5﹣4sin2θ.
,(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为(ρ﹣2cosθ)2=5﹣4sin2θ.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相切,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com