练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知-5sin2α+sin2β=3sinα，则y=sin2α+sin2β函数的最小值为0．

    分析 由-5sin2α+sin2β=3sinα，可得sin2β=5sin2α+3sinα≥0，可得sinα∈[0，1]，转化为二次函数求解最小值即可．

    解答 解：由-5sin2α+sin2β=3sinα，可得sin2β=5sin2α+3sinα∈[0，1]，
    可得sinα∈[$-\frac{3+\sqrt{29}}{10}，-\frac{3}{5}$]∪[0，$\frac{-3+\sqrt{29}}{10}$]
    那么y=sin2α+sin2β=6sin2α+3sinα=6（sinα+$\frac{1}{2}$）2$-\frac{1}{4}$
    当sinα=0时，y取得最小值为0．
    故答案为0．

    点评 本题主要考查了同角三角函数关系式和三角函数的有界性的应用，属于基本知识的考查．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．在棱长为1的正方体ABCD-A1B1C1D1中，异面直线AD1与DC1所成角的大小为（　　）
    A．$\frac{2π}{3}$B．$\frac{π}{2}$C．$\frac{π}{3}$D．$\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知tan=$\frac{1}{2}$，$\frac{2sinx+3cosx}{cosx-sinx}$的值为（　　）
    A．-7B．8C．-8D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

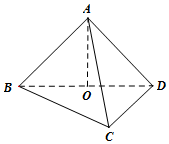    2．（文科）设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O，
    AC=BC=1，CD=$\sqrt{2}$，
    求（1）AC与平面BCD所成角的大小；
    （2）异面直线AB和CD的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若函数f（x）=x2+bx+c的图象的对称轴为x=2，则函数f（x）的导函数f'（x）的图象不经过（　　）
    A．第一象限B．第二象限C．第三象限D．第三象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=2cos2x+2$\sqrt{3}$sinxcosx-1（x∈R）．
    （1）把f（x）化简成f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的形式
    （2）求函数f（x）的单调增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知f（x）=x3+x2f′（2）+2lnx，则f′（1）=（　　）
    A．$\frac{3}{2}$B．$-\frac{11}{3}$C．3D．-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知函数f（x）=2ln（3x）+8x，则$\underset{lim}{△x→0}$$\frac{f（1-2△x）-f（1）}{△x}$的值为（　　）
    A．10B．-10C．-20D．20

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．曲线$\sqrt{1-{{（x-1）}^2}}$=|y-1|-2与直线y=k（x-4）+1有两个不同交点，则实数k的取值范围是[1，$\frac{3-\sqrt{3}}{4}$）∪（$\frac{\sqrt{3}-3}{4}$，-1]． 

    查看答案和解析>>

    同步练习册答案