
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如图.

(1)求频率分布直方图中a的值;
(2)估计总体中成绩落在[50,60)中的学生人数;
(3)根据频率分布直方图估计20名学生数学考试成绩的众数,平均数;
【答案】(1)0.005 (2)2人 (3)75 分 ,76.5分
【解析】
(1)由频率分布直方图列方程能求出a;
(2)由频率分布直方图得成绩落在[50,60)中的频率为0.1,由此能估计总体中成绩落在[50,60)中的学生人数;
(3)根据频率分布直方图能估计20名学生数学考试成绩的众数和平均数.
(1)由频率分布直方图得:
(2a+3a+7a+6a+2a)×10=1,
解得a=0.005.
(2)由频率分布直方图得成绩落在[50,60)中的频率为2a×10=0.1,
∴估计总体中成绩落在[50,60)中的学生人数为:
20×0.1=2人.
(3)根据频率分布直方图估计20名学生数学考试成绩的众数为:![]() 75,
75,
平均数为:2×0.005×10×55+3×0.005×10×65+7×0.005×10×75+6×0.005×10×85+2×0.005×10×95=76.5.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为3,中位数为4 B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3 D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量(百件)与销售单价x(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.

(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润?(注:利润=收入-支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任为了对本班学生的月考成绩进行分析,从全班40名同学中随机抽取一个容量为6的样本进行分析.随机抽取6位同学的数学、物理分数对应如表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学分数x | 60 | 70 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 80 | 88 | 90 | 85 | 95 |
(1)根据上表数据用散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?
(2)如果具有线性相关性,求出线性回归方程(系数精确到0.1);如果不具有线性相关性,请说明理由.
(3)如果班里的某位同学数学成绩为50,请预测这位同学的物理成绩。
![]() (附
(附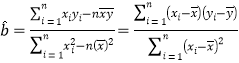 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y= 4cos2x+4![]() sinxcosx-2,(x∈R)
sinxcosx-2,(x∈R)
(1)求函数的最小正周期;
(2)求函数的最大值及其相对应的x值;
(3)写出函数的单调增区间;
(4)写出函数的对称轴
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1中,底面ABC为等腰直角三角形,AB=AC=1,BB1=2,∠ABB1=60°.
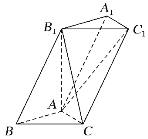
(I) 证明:AB⊥平面AB1C;
(II) 若B1C=2,求AC1与平面BCB1所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com