
【题目】如图,四棱锥![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
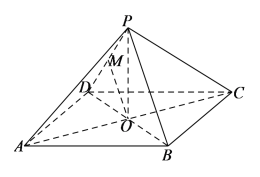
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用中位线的性质得出![]() ,然后利用线面平行的判定定理可证得结论;
,然后利用线面平行的判定定理可证得结论;
(2)推导出![]() 平面
平面![]() ,可得出
,可得出![]() ,再由
,再由![]() 结合线面垂直的判定定理可得出
结合线面垂直的判定定理可得出![]() 平面
平面![]() ,最后利用面面垂直的判定定理可证得结论;
,最后利用面面垂直的判定定理可证得结论;
(3)以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 轴建立空间直角坐标系,利用空间向量法能计算出二面角
轴建立空间直角坐标系,利用空间向量法能计算出二面角![]() 的余弦值.
的余弦值.
(1)![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 为
为![]() 中点,
中点,
![]() 为
为![]() 中点,
中点,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 为
为![]() 、
、![]() 中点,
中点,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
(3)以点![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴,过
轴,过![]() 且与平面
且与平面![]() 垂直的直线为
垂直的直线为![]() 轴,建立如图所示空间直角坐标系
轴,建立如图所示空间直角坐标系![]() ,
,
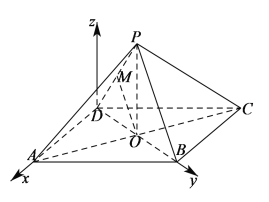
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 和平面
和平面![]() 的法向量分别为
的法向量分别为![]() ,
,![]() ,
,
由 ,得
,得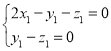 ,令
,令![]() ,可得
,可得![]() ,
,
由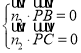 ,得
,得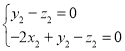 ,令
,令![]() ,可得
,可得![]() ,
,
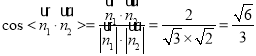 ,
,
由图形可知,二面角![]() 的平面角为钝角,它的余弦值为
的平面角为钝角,它的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 单调递增,下述三个结论:①
单调递增,下述三个结论:①![]() 的取值范围是
的取值范围是![]() ;②
;②![]() 在
在![]() 存在零点;③
存在零点;③![]() 在
在![]() 至多有4个极值点.其中所有正确结论的编号是( )
至多有4个极值点.其中所有正确结论的编号是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 为平行四边形,
为平行四边形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
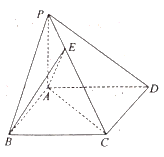
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)在侧棱![]() 上是否存在点E,使
上是否存在点E,使![]() 与底面
与底面![]() 所成的角为45°?若存在,求
所成的角为45°?若存在,求![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的离心率为
)的离心率为![]() ,且椭圆C的中心O关于直线
,且椭圆C的中心O关于直线![]() 的对称点落在直线
的对称点落在直线![]() 上.
上.
(1)求椭圆C的方程;
(2)设P![]() ,M、N是椭圆C上关于x轴对称的任意两点,连接
,M、N是椭圆C上关于x轴对称的任意两点,连接![]() 交椭圆C于另一点E,求直线
交椭圆C于另一点E,求直线![]() 的斜率取值范围,并证明直线
的斜率取值范围,并证明直线![]() 与x轴相交于定点.
与x轴相交于定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: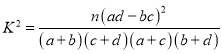 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年新型冠状病毒疫情爆发,贵州省教育厅号召全体学生“停课不停学”.自
年新型冠状病毒疫情爆发,贵州省教育厅号召全体学生“停课不停学”.自![]() 月
月![]() 日起,高三年级学生通过收看“阳光校园·空中黔课”进行线上网络学习.为了检测线上网络学习效果,某中学随机抽取
日起,高三年级学生通过收看“阳光校园·空中黔课”进行线上网络学习.为了检测线上网络学习效果,某中学随机抽取![]() 名高三年级学生做“是否准时提交作业”的问卷调查,并组织了一场线上测试,调查发现有
名高三年级学生做“是否准时提交作业”的问卷调查,并组织了一场线上测试,调查发现有![]() 名学生每天准时提交作业,根据他们的线上测试成绩得频率分布直方图(如图
名学生每天准时提交作业,根据他们的线上测试成绩得频率分布直方图(如图![]() 所示);另外
所示);另外![]() 名学生偶尔没有准时提交作业,根据他们的线上测试成绩得茎叶图(如图
名学生偶尔没有准时提交作业,根据他们的线上测试成绩得茎叶图(如图![]() 所示,单位:分)
所示,单位:分)
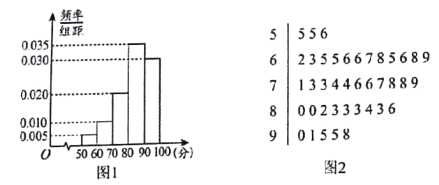
(1)成绩不低于![]() 分为
分为![]() 等,低于
等,低于![]() 分为非
分为非![]() 等.完成以下列联表,并判断是否有
等.完成以下列联表,并判断是否有![]() 以上的把握认为成绩取得
以上的把握认为成绩取得![]() 等与每天准时提交作业有关?
等与每天准时提交作业有关?
准时提交作业与成绩等次列联表 | 单位:人 | ||
A等 | 非A等 | 合计 | |
每天准时提交作业 | |||
偶尔没有准时提交作业 | |||
合计 | |||
(2)成绩低于![]() 分为不合格,从这
分为不合格,从这![]() 名学生里成绩不合格的学生中再抽取
名学生里成绩不合格的学生中再抽取![]() 人,其中每天准时提交作业的学生人数为
人,其中每天准时提交作业的学生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附: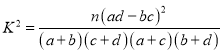
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下列材料,回答所提问题:设函数![]() ,①
,①![]() 的定义域为
的定义域为![]() ,其图像是一条连续不断的曲线;②
,其图像是一条连续不断的曲线;②![]() 是偶函数;③
是偶函数;③![]() 在
在![]() 上不是单调函数;④
上不是单调函数;④![]() 恰有
恰有![]() 个零点,写出符合上述①②④条件的一个函数的解析式是______;写出符合上述所有条件的一个函数的解析式是______.
个零点,写出符合上述①②④条件的一个函数的解析式是______;写出符合上述所有条件的一个函数的解析式是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,新型冠状病毒肺炎(COVID-19)在我国爆发,全国人民团结一心、积极抗疫,为全世界疫情防控争取了宝贵的时间,积累了丰富的经验.某研究小组为了研究某城市肺炎感染人数的增长情况,在官方网站.上搜集了7组数据,并依据数据制成如下散点图:
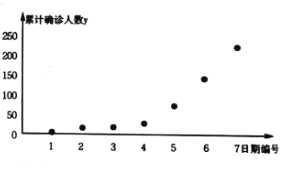
图中![]() 表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型
表示日期代号(例如2月1日记为“1”,2月2日记为“2”,以此类推).通过对散点图的分析,结合病毒传播的相关知识,该研究小组决定用指数型函数模型![]() 来拟合,为求出
来拟合,为求出![]() 关于
关于![]() 的回归方程,可令
的回归方程,可令![]() ,则
,则![]() 与
与![]() 线性相关.初步整理后,得到如下数据:
线性相关.初步整理后,得到如下数据:![]() ,
,![]() .
.
(1)根据所给数据,求出![]() 关于
关于![]() 的线性回归方程:
的线性回归方程:
(2)求![]() 关于
关于![]() 的回归方程;若防控不当,请问
的回归方程;若防控不当,请问![]() 为何值时,累计确诊人数的预报值将超过1000人?(参考数据:
为何值时,累计确诊人数的预报值将超过1000人?(参考数据:![]() ,结果保留整数)
,结果保留整数)
附:对于一组数据![]() ,其线性回归方程
,其线性回归方程![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为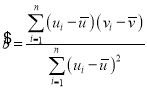 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com