
分析 (1)直接在数列递推式中取n=1求得a1的值;
(2)当n≥2时,把Sn用含有Sn-1的代数式表示,然后利用定义法证明数列{$\frac{1}{{S}_{n}-1}$}是等差数列;
(3)由(2)求出Sn,代入bn=$\frac{n+1}{n+2}$Sn,再利用累积法求得数列{bn}列的前2015项之积.
解答 (1)解:当n=1时,由已知可得${{a}_{1}}^{2}-2{a}_{1}-{{a}_{1}}^{2}+1=0$,解得${a}_{1}=\frac{1}{2}$;
(2)证明:∵Sn2-2Sn-an•Sn+1=0,
当n≥2时,an=Sn-Sn-1,代入上式,得:SnSn-1-2Sn+1=0.
∴Sn与Sn-1(n≥2)的关系式为${S}_{n}=\frac{1}{2-{S}_{n-1}}$,
∴当n≥2时,$\frac{1}{{S}_{n}-1}-\frac{1}{{S}_{n-1}-1}=\frac{1}{\frac{1}{2-{S}_{n-1}}-1}-\frac{1}{{S}_{n-1}-1}$=$\frac{2-{S}_{n-1}}{{S}_{n-1}-1}-\frac{1}{{S}_{n-1}-1}=-1$.
∴数列{$\frac{1}{{S}_{n}-1}$}是以$\frac{1}{{S}_{1}-1}=-2$为首项,-1为公差的等差数列.
(3)解:由(2)可知$\frac{1}{{S}_{n}-1}=-2-(n-1)$,∴${S}_{n}=\frac{n}{n+1}$,
∴${b}_{n}=\frac{n+1}{n+2}•{S}_{n}=\frac{n}{n+2}$,
∴${b}_{1}{b}_{2}…{b}_{2015}=\frac{1}{3}•\frac{2}{4}•\frac{3}{5}…\frac{2014}{2016}•\frac{2015}{2017}=\frac{1}{2033136}$.
点评 本题考查数列递推式,考查了等差关系的确定,训练了累积法求数列的通项公式,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | x2+y2+10y=0 | B. | x2+y2-10y=0 | C. | x2+y2+10x=0 | D. | x2+y2-10x=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
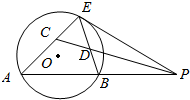 如图,过圆外一点P的直线交圆O于A、B两点,PE是圆O的切线,CP平分∠APE,分别与AE、BE交于点C,D.
如图,过圆外一点P的直线交圆O于A、B两点,PE是圆O的切线,CP平分∠APE,分别与AE、BE交于点C,D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至多一对 | B. | 至多2对 | C. | 有无穷对 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,6} | B. | {1,3,5} | C. | {2,4} | D. | {2,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com