
【题目】已知二次函数f(x)=ax2+bx+c(a≠0)的图象过点(0,1)且与x轴有唯一的交点(﹣1,0).
(1)求f(x)的表达式;
(2)在(1)的条件下,设函数F(x)=f(x)﹣mx,若F(x)在区间[﹣2,2]上是单调函数,求实数m的取值范围;
(3)设函数g(x)=f(x)﹣kx,x∈[﹣2,2],记此函数的最小值为h(k),求h(k)的解析式.
【答案】
(1)解:依题意得c=1, ![]() ,b2﹣4ac=0
,b2﹣4ac=0
解得a=1,b=2,c=1,
从而f(x)=x2+2x+1;
(2)解:F(x)=x2+(2﹣m)x+1图象的对称轴为直线 ![]() ,图象开口向上,
,图象开口向上,
当 ![]() 或
或 ![]() ,即m≤﹣2或m≥6时,F(x)在[﹣2,2]上单调,
,即m≤﹣2或m≥6时,F(x)在[﹣2,2]上单调,
故实数m的取值范围为(﹣∞,﹣2]∪[6,+∞);
(3)解:g(x)=x2+(2﹣k)x+1图象的对称轴为直线 ![]() ,图象开口向上
,图象开口向上
当 ![]() ,即k≤﹣2时,F(x)在[﹣2,2]上单调递增,
,即k≤﹣2时,F(x)在[﹣2,2]上单调递增,
此时函数F(x)的最小值g(k)=F(﹣2)=2k+1
当 ![]() 即﹣2<k≤6时,F(x)在
即﹣2<k≤6时,F(x)在 ![]() 上递减,在
上递减,在 ![]() 上递增
上递增
此时函数F(x)的最小值 ![]() ;
;
当 ![]() 即k>6时,F(x)在[﹣2,2]上单调递减,
即k>6时,F(x)在[﹣2,2]上单调递减,
此时函数F(x)的最小值g(k)=F(2)=9﹣2k;
综上,函数F(x)的最小值 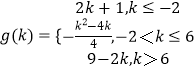
【解析】(1)依题意得c=1, ![]() ,b2﹣4ac=0,解方程组求出a,b,c值,可得f(x)的表达式;(2)函数F(x)=x2+(2﹣m)x+1图象的对称轴为直线
,b2﹣4ac=0,解方程组求出a,b,c值,可得f(x)的表达式;(2)函数F(x)=x2+(2﹣m)x+1图象的对称轴为直线 ![]() ,图象开口向上,若F(x)在区间[﹣2,2]上是单调函数,则区间在对称轴的一侧,进而得到实数m的取值范围;(3)g(x)=x2+(2﹣k)x+1图象的对称轴为直线
,图象开口向上,若F(x)在区间[﹣2,2]上是单调函数,则区间在对称轴的一侧,进而得到实数m的取值范围;(3)g(x)=x2+(2﹣k)x+1图象的对称轴为直线 ![]() ,图象开口向上,不同情况下g(x)在区间[﹣2,2]上单调性,进而可得函数的最小值为h(k)的解析式.
,图象开口向上,不同情况下g(x)在区间[﹣2,2]上单调性,进而可得函数的最小值为h(k)的解析式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了解消费者购物情况,某购物中心在电脑小票中随机抽取![]() 张进行统计,将结果分成6组,分别是:
张进行统计,将结果分成6组,分别是: ![]() ,
, ![]() ,制成如下所示的频率分布直方图(假设消费金额均在
,制成如下所示的频率分布直方图(假设消费金额均在![]() 元的区间内).
元的区间内).
(1)若在消费金额为![]() 元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票来自
元区间内按分层抽样抽取6张电脑小票,再从中任选2张,求这2张小票来自![]() 元和
元和![]() 元区间(两区间都有)的概率;
元区间(两区间都有)的概率;
(2)为做好春节期间的商场促销活动,商场设计了两种不同的促销方案.

方案一:全场商品打八五折.
方案二:全场购物满100元减20元,满300元减80元,满500元减120元,以上减免只取最高优惠,不重复减免.利用直方图的信息分析:哪种方案优惠力度更大,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为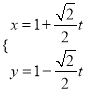 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 点的直角坐标为
点的直角坐标为![]() .
.
(1)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下说法:①不共面的四点中,任意三点不共线;
②有三个不同公共点的两个平面重合;
③没有公共点的两条直线是异面直线;
④分别和两条异面直线都相交的两条直线异面;
⑤一条直线和两条异面直线都相交,则它们可以确定两个平面.
其中正确结论的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从抛物线y2=32x上各点向x轴作垂线,其垂线段中点的轨迹为E.
(1)求轨迹E的方程;
(2)已知直线l:y=k(x-2)(k>0)与轨迹E交于A,B两点,且点F(2,0),若|AF|=2|BF|,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]() ,点
,点![]() 在圆
在圆![]() 上,点
上,点![]() 在圆
在圆![]() 上.
上.
(1)求![]() 的最小值;
的最小值;
(2)直线![]() 上是否存在点
上是否存在点![]() ,满足经过点
,满足经过点![]() 由无数对相互垂直的直线
由无数对相互垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,并且直线
相交,并且直线![]() 被圆
被圆![]() 所截得的弦长等于直线
所截得的弦长等于直线![]() 被圆
被圆![]() 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数 ![]() 是奇函数.
是奇函数.
(1)求a值;
(2)判断并证明该函数在定义域R上的单调性;
(3)设关于x的函数F(x)=f(4x﹣b)+f(﹣2x+1)有零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x|(2x)2﹣62x+8≤0},函数f(x)=log2x(x∈A).
(1)求函数f(x)的定义域;
(2)若函数h(x)=[f(x)]2﹣log2(2x),求函数h(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com