
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,C为椭圆上位于第一象限内的一点.
,C为椭圆上位于第一象限内的一点.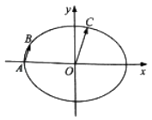
(1)若点C的坐标为(2, ![]() ),求a,b的值;
),求a,b的值;
(2)设A为椭圆的左顶点,B为椭圆上一点,且 ![]() =
= ![]() ,求直线AB的斜率.
,求直线AB的斜率.
【答案】
(1)解:由题意可知:椭圆的离心率e= ![]() =
= ![]() =
= ![]() ,则
,则 ![]() =
= ![]() ,①
,①
由点C在椭圆上,将(2, ![]() )代入椭圆方程,
)代入椭圆方程, ![]() ,②
,②
解得:a2=9,b2=5,
∴a=3,b= ![]() ,
,
(2)方法一:由(1)可知: ![]() =
= ![]() ,则椭圆方程:5x2+9y2=5a2,
,则椭圆方程:5x2+9y2=5a2,
设直线OC的方程为x=my(m>0),B(x1,y1),C(x2,y2),
![]() ,消去x整理得:5m2y2+9y2=5a2,
,消去x整理得:5m2y2+9y2=5a2,
∴y2= ![]() ,由y2>0,则y2=
,由y2>0,则y2= ![]() ,
,
由 ![]() =
= ![]() ,则AB∥OC,设直线AB的方程为x=my﹣a,
,则AB∥OC,设直线AB的方程为x=my﹣a,
则 ![]() ,整理得:(5m2+9)y2﹣10amy=0,
,整理得:(5m2+9)y2﹣10amy=0,
由y=0,或y1= ![]() ,
,
由 ![]() =
= ![]() ,则(x1+a,y1)=(
,则(x1+a,y1)=( ![]() x2,
x2, ![]() y2),
y2),
则y2=2y1,
则 ![]() =2×
=2× ![]() ,(m>0),
,(m>0),
解得:m= ![]() ,
,
则直线AB的斜率 ![]() =
= ![]() ;
;
方法二:由(1)可知:椭圆方程5x2+9y2=5a2,则A(﹣a,0),
B(x1,y1),C(x2,y2),
由 ![]() =
= ![]() ,则(x1+a,y1)=(
,则(x1+a,y1)=( ![]() x2,
x2, ![]() y2),则y2=2y1,
y2),则y2=2y1,
由B,C在椭圆上,
∴ 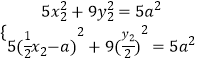 ,解得:
,解得: 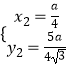 ,
,
则直线直线AB的斜率k= ![]() =
= ![]() .
.
直线AB的斜率 ![]() .
.
【解析】(1)根据离心率表示出![]() ,根据点C在椭圆上,代入即可得到a,b的值,(2)方法一:根据(1)得到椭圆方程,设直线OC的方程为x=my(m>0),B(x1,y1),C(x2,y2),联立方程利用韦达定理可解出m的值,方法二:根据(1)得到椭圆方程,则A(﹣a,0),
,根据点C在椭圆上,代入即可得到a,b的值,(2)方法一:根据(1)得到椭圆方程,设直线OC的方程为x=my(m>0),B(x1,y1),C(x2,y2),联立方程利用韦达定理可解出m的值,方法二:根据(1)得到椭圆方程,则A(﹣a,0),
B(x1,y1),C(x2,y2),由向量关系和B、C在椭圆上,解出x2,y2,可得直线AB的斜率.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】要想得到函数 ![]() 的图象,只需将函数y=sinx的图象上所有的点( )
的图象,只需将函数y=sinx的图象上所有的点( )
A.先向右平移 ![]() 个单位长度,再将横坐标伸长为原来的2倍,纵坐标不变
个单位长度,再将横坐标伸长为原来的2倍,纵坐标不变
B.先向右平移 ![]() 个单位长度,横坐标缩短为原来的
个单位长度,横坐标缩短为原来的 ![]() 倍,纵坐标不变
倍,纵坐标不变
C.横坐标缩短为原来的 ![]() 倍,纵坐标不变,再向右平移
倍,纵坐标不变,再向右平移 ![]() 个单位长度
个单位长度
D.横坐标变伸长原来的2倍,纵坐标不变,再向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB= ![]() ,AF=1,G为线段AD上的任意一点.
,AF=1,G为线段AD上的任意一点. 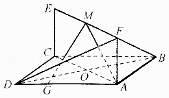
(1)若M是线段EF的中点,证明:平面AMG⊥平面BDF;
(2)若N为线段EF上任意一点,设直线AN与平面ABF,平面BDF所成角分别是α,β,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]()
![]() ,其中
,其中 ![]() =(2cosx,﹣
=(2cosx,﹣ ![]() sin2x),
sin2x), ![]() =(cosx,1),x∈R.
=(cosx,1),x∈R.
(1)求f(x)的单调递减区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=﹣1,a= ![]() ,且向量
,且向量 ![]() =(3,sinB)与
=(3,sinB)与 ![]() =(2,sinC)共线,求边长b和c的值.
=(2,sinC)共线,求边长b和c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x﹣ ![]() )+2cos2x,将函数y=f(x)的图象向右平移
)+2cos2x,将函数y=f(x)的图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
A.(﹣ ![]() ,1)
,1)
B.(﹣ ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=2px(p>0)的焦点为F,准线为L,A、B是抛物线上的两个动点,且满足∠AFB= ![]() .设线段AB的中点M在L上的投影为N,则
.设线段AB的中点M在L上的投影为N,则 ![]() 的最大值是( )
的最大值是( )
A.![]()
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程: ![]() (t为参数),曲线C的参数方程:
(t为参数),曲线C的参数方程: ![]() (α为参数),且直线交曲线C于A,B两点.
(α为参数),且直线交曲线C于A,B两点.
(Ⅰ)将曲线C的参数方程化为普通方程,并求θ= ![]() 时,|AB|的长度;
时,|AB|的长度;
(Ⅱ)已知点P:(1,0),求当直线倾斜角θ变化时,|PA||PB|的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x , 函数g(x)=log
)x , 函数g(x)=log ![]() x.
x.
(1)若g(ax2+2x+1)的定义域为R,求实数a的取值范围;
(2)当x∈[( ![]() )t+1 , (
)t+1 , ( ![]() )t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
)t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
(3)是否存在非负实数m,n,使得函数y=log ![]() f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池ABCD及其矩形附属设施EFGH,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为O,半径为R,矩形的一边AB在直径上,点C,D,G,H在圆周上,E,F在边CD上,且 ![]() ,设∠BOC=θ.
,设∠BOC=θ.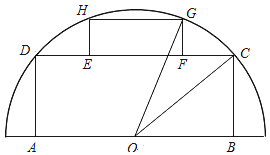
(1)记游泳池及其附属设施的占地面积为f(θ),求f(θ)的表达式;
(2)怎样设计才能符合园林局的要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com