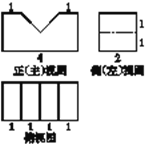
【题目】一个空间几何体的三视图如图所示，则这个几何体的表面积为( )
A. 26＋4
B. 27＋4
C. 34＋4
D. 17＋2
【答案】C
【解析】由三视图可知，该几何体的直观图如下图所示，是由两个相同的直五棱柱组合而成，故这个几何体的表面积为S＝
×2＋2×2＋1×2＋
×2＋2×2×2＝34＋4
.
点睛:思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝ln x＋ax－
＋b.
(1)若函数g(x)＝f(x)＋
为减函数，求实数a的取值范围；
(2)若f(x)≤0恒成立，证明：a≤1－b.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地棚户区改造建筑用地平面示意图如图所示，经规划调研确定，棚改规划建筑用地区域近似为圆面，该圆面的内接四边形ABCD是原棚户区建筑用地，测量可知边界AB＝AD＝4万米，BC＝6万米，CD＝2万米．
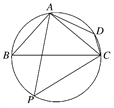
(1)请计算原棚户区建筑用地ABCD的面积及AC的长；
(2)因地理条件的限制，边界AD，DC不能变更，而边界AB，BC可以调整，为了提高棚户区建筑用地的利用率，请在
上设计一点P，使得棚户区改造后的新建筑用地APCD的面积最大，并求出最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某项竞赛分为初赛、复赛、决赛三个阶段进行，每个阶段选手要回答一个问题．规定正确回答问题者进入下一阶段竞赛，否则即遭淘汰．已知某选手通过初赛、复赛、决赛的概率分别是
且各阶段通过与否相互独立．
(1)求该选手在复赛阶段被淘汰的概率；
(2)设该选手在竞赛中回答问题的个数为ξ，求ξ的分布列与均值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB＝4，AD＝2，E在DC边上，且DE＝1，将△ADE沿AE折到△AD′E的位置，使得平面AD′E⊥平面ABCE.
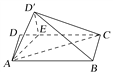
(1)求证：AE⊥BD′；
(2)求三棱锥A－BCD′的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(导学号：05856287)
已知点A(0,1)与B(
， 
)都在椭圆C： 
(a＞b＞0)上，直线AB交x轴于点M.
(Ⅰ)求椭圆C的方程，并求点M的坐标；
(Ⅱ)设O为原点，点D与点B关于x轴对称，直线AD交x轴于点N.问：y轴上是否存在点E，使得∠OEM＝∠ONE？若存在，求点E的坐标；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在极坐标系中，设圆
：＝4 cos 与直线l：＝
(∈R)交于A，B两点．
（Ⅰ）求以AB为直径的圆
的极坐标方程；
（Ⅱ）在圆
任取一点
，在圆
上任取一点
，求
的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
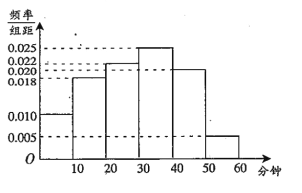
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系，对该校200名学生的课外体育锻炼平均每天运动的时间（单位：分钟）进行调查，将收集的数据分成
六组，并作出频率分布直方图（如图），将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
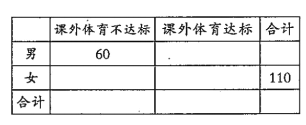
(1)请根据直方图中的数据填写下面的
列联表，并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关？
（2）现按照“课外体育达标”与“课外体育不达标”进行分层抽样，抽取8人，再从这8名学生中随机抽取3人参加体育知识问卷调查，记“课外体育不达标”的人数为
，求
的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高中一年级600名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成
组：[20,30），[30,40），┄，[80,90]，并整理得到如下频率分布直方图：
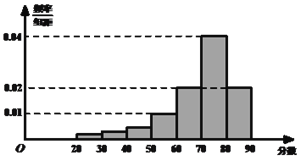
（1）从总体的600名学生中随机抽取一人，估计其分数小于70的概率；
（2）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40,50）内的人数；
（3）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com