
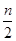 );如果n是奇数,则将它乘3加1(即
);如果n是奇数,则将它乘3加1(即 ),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为6,按照上述变换规则,我们可以得到一个数列:6,3,10,5,16,8,4,2,1.对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:
),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为6,按照上述变换规则,我们可以得到一个数列:6,3,10,5,16,8,4,2,1.对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究: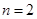 ,则按照上述规则施行变换后的第8项为 .
,则按照上述规则施行变换后的第8项为 . (首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则
(首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则 的所有不同值的个数为 .
的所有不同值的个数为 . 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
| A.若a与b共线,则a☉b=0 |
| B.a☉b=b☉a |
| C.对任意的λ∈R,有(λa)☉b=λ(a☉b) |
| D.(a☉b)2+(a·b)2=|a|2|b|2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 个图形包含的小圆圈个数为
个图形包含的小圆圈个数为 ,则(Ⅰ)
,则(Ⅰ) = ;(Ⅱ)
= ;(Ⅱ) 的个位数字为 .
的个位数字为 .
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
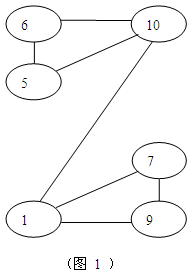
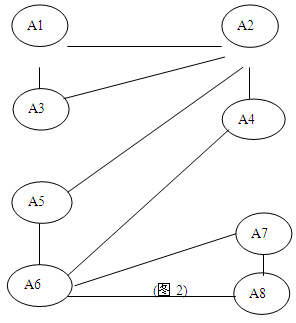
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.190 | B.191 | C.192 | D.193 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com