
【题目】设函数 ![]() (
( ![]() 为常数,e=2.71828……是自然对数的底数).
为常数,e=2.71828……是自然对数的底数).
(1)当 ![]() 时,求函数
时,求函数 ![]() 的单调区间;
的单调区间;
(2)若函数 ![]() 在
在 ![]() 内存在两个极值点,求
内存在两个极值点,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:函数 ![]() 的定义域为
的定义域为 ![]()
![]()
由 ![]() 可得
可得 ![]() ,
,
所以当 ![]() 时,
时, ![]() ,函数
,函数 ![]() 单调递减;
单调递减;
当 ![]() 时,
时, ![]() ,函数
,函数 ![]() 单调递增;
单调递增;
所以 ![]() 的单调递减区间为
的单调递减区间为 ![]() 单调递增区间为
单调递增区间为 ![]()
(2)解:由1知, ![]() 时,函数
时,函数 ![]() 在
在 ![]() 内单调递减,
内单调递减,
故 ![]() 在
在 ![]() 内不存在极值点;
内不存在极值点;
当 ![]() 时,设函数
时,设函数 ![]() ,,
,,
因为 ![]() ,
,
当 ![]() 时,当
时,当 ![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
故 ![]() 在
在 ![]() 内不存在两个极值点;
内不存在两个极值点;
当 ![]() 时,得
时,得 ![]() 时,
时, ![]() ,函数
,函数 ![]() 单调递减;
单调递减;
![]() 时,
时, ![]() ,函数
,函数 ![]() 单调递增;
单调递增;
所以函数 ![]() 的最小值为
的最小值为 ![]() ,
,
函数 ![]() 在
在 ![]() 内存在两个极值点,
内存在两个极值点,
当且仅当 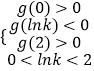 ,解得
,解得 ![]() .
.
综上所述,函数 ![]() 在
在 ![]() 内存在两个极值点时,k的取值范围为
内存在两个极值点时,k的取值范围为 ![]()
【解析】(1)根据题意结合已知条件求出原函数的导函数利用导函数在指定区间上的的正负情况得出原函数的增减性以及增减区间。(2)函数f(x) 在( 0 , 2 ) 内存在两个极值点,等价于它的导函数f‘(x) 在 ( 0 , 2 ) 内存在两个不同的零点。
【考点精析】掌握利用导数研究函数的单调性和函数的零点是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.
在这个区间单调递减;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.


科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() 为线段
为线段![]() (含端点)上一个动点,设
(含端点)上一个动点,设![]() 对于函数
对于函数![]() ,给出以下三个结论:
,给出以下三个结论:
①当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ;
;
②对于任意的![]() ,均有
,均有![]() ;
;
③对于任意的![]() ,函数
,函数![]() 的最大值均为4.
的最大值均为4.
其中所有正确的结论序号为__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为 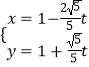 (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为 ![]() (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为 ![]() ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年,在国家创新驱动战略下,北斗系统作为一项国家高科技工程,一个开放型的创新平台,1400多个北斗基站遍布全国,上万台设备组成星地“一张网”,国内定位精度全部达到亚米级,部分地区达到分米级,最高精度甚至可以达到厘米或毫米级。最近北斗三号工程耗资![]() 元建成一大型设备,已知这台设备维修和消耗费用第一年为
元建成一大型设备,已知这台设备维修和消耗费用第一年为![]() 元,以后每年增加
元,以后每年增加![]() 元(
元(![]() 是常数),用
是常数),用![]() 表示设备使用的年数,记设备年平均维修和消耗费用为
表示设备使用的年数,记设备年平均维修和消耗费用为![]() ,即
,即![]() (设备单价
(设备单价![]() 设备维修和消耗费用)
设备维修和消耗费用)![]() 设备使用的年数.
设备使用的年数.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() ,
, ![]() 时,求这种设备的最佳更新年限.
时,求这种设备的最佳更新年限.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为  (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为 ![]() (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为 ![]() ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电脑公司有6名产品推销员,其中工作年限与年推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 4 | 5 | 6 |
(1)请画出上表数据的散点图;

(2)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线C1 ![]() (t为参数),C2
(t为参数),C2 ![]() (θ为参数),
(θ为参数),
(Ⅰ)当α= ![]() 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(Ⅱ)过坐标原点O做C1的垂线,垂足为A,P为OA中点,当α变化时,求P点的轨迹的参数方程,并指出它是什么曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com