Question

已知函数f（x）=2acos²x+bsinxcosx-，且f（0）=，f（）=．
（Ⅰ）函数f（x）的图象经过怎样的平移才能使其对应的函数成为奇函数？
（Ⅱ）函数f（x）的图象经过怎样的平移后得到y=cosx．

Answer 1

解：由f（0）=，f（）=得：a=，b=1，所以，函数f（x）=2acos²x+bsinxcosx-=sin（2x+），
（Ⅰ）思路一：函数y=f（x）的图象关于（-，0）对称，向右平移个单位后图象关于原点对称即为奇函数（平移的方法不唯一，因为函数y=f（x）的图象对称中心不唯一）；
思路二：若函数f（x）的图象向右平移m个单位得到函数y=sin（2x-2m+），要使其为奇函数，则x=0时函数值为0（奇函数图象关于原点对称），即-2m+=kπ，k∈Z?m=-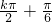，k∈Z，随k的取值不同可以得到不同的m的值，回答其中任一个即可．（运算量虽大一些，但更具一般性）．
（Ⅱ）f（x）=sin（2x+）=cos（-2x）=cos（2x-）=cos[2（x-）]，方案一：先左移（x变成x+）得到函数y=cos2x，再纵坐标不变横坐标变为原来的2倍（x变成）得到函数y=cosx；
方案二：先纵坐标不变横坐标变为原来的2倍（x变成）得到函数y=cos（x-），再左移（x变成x+）得到函数y=cosx．
分析：利用f（0）=，f（）=求得：a=，b=1，然后化简函数利用降次、“合二为一”后得f（x）=sin（2x+），
（Ⅰ）思路一：函数向右平移个单位后图象关于原点对称即为奇函数．
思路二：好的图象向右平移，使之化为y=sin2x的图象即可．
（Ⅱ）利用诱导公式化简f（x）=sin（2x+）=cos[2（x-）]，方案一：选向左平移，然后再伸缩变换．
方案二：先伸缩变换，然后向左平移，注意平移时x的系数问题．
点评：（ⅰ）图象变换的问题要特别注意题目要求由谁变到谁，不要搞错了方向；（ⅱ）变换的源头和结果需化为同名的三角函数且角变量的系数同号（用诱导公式）才能实施；（ⅲ）如果已知变换的结果探究变换的源头，可以“倒行逆施”．