
在直角坐标系 中,曲线
中,曲线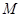 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系的原点
为参数),若以直角坐标系的原点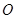 为极点,
为极点, 轴的正半轴为极轴建立极坐标,曲线
轴的正半轴为极轴建立极坐标,曲线 的极坐标方程为
的极坐标方程为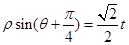 (其中
(其中 为常数).
为常数).
(1)若曲线 与曲线
与曲线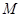 只有一个公共点,求
只有一个公共点,求 的取值范围;
的取值范围;
(2)当 时,求曲线
时,求曲线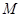 上的点与曲线
上的点与曲线 上的点的最小距离
上的点的最小距离
(1)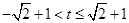 或
或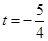 ;(2)
;(2)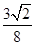 .
.
解析试题分析:本题考查极坐标与直角坐标之间的转化,参数方程与普通方程之间的转化,考查学生的转化能力和计算能力,考查数形结合思想.第一问,把参数方程和极坐标方程先进行转化,再利用数形结合解题;第二问,考查点到直线的距离公式,利用配方法求最小值.
试题解析:(1)曲线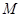 可化为
可化为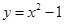 ,
,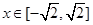 ,
,
曲线 可化为
可化为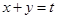 ,
,
若曲线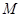 ,
, 只有一个公共点,
只有一个公共点,
则当直线 过点
过点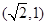 时满足要求,此时
时满足要求,此时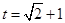 ,
,
并且向左下方平行运动直到过点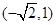 之前总是保持只有一个公共点,
之前总是保持只有一个公共点,
当直线N过点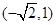 时,此时
时,此时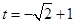 ,
,
所以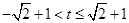 满足要求;
满足要求;
再接着从过点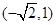 开始向左下方平行运动直到相切之前总有两个公共点,相切时仍然只有一个公共点,联立
开始向左下方平行运动直到相切之前总有两个公共点,相切时仍然只有一个公共点,联立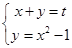 ,得
,得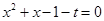 ,
,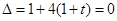 ,解得
,解得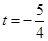 ,
,
综上可求得 的取值范围是
的取值范围是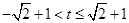 或
或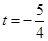 .(5分)
.(5分)
(2)当 时,直线
时,直线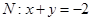 ,
,
设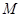 上的点为
上的点为 ,
,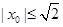 ,
,
则曲线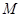 上的点到直线
上的点到直线 的距离为
的距离为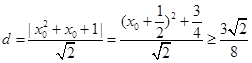 ,
,
当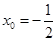 时取等号,满足
时取等号,满足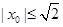 ,所以所求的最小距离为
,所以所求的最小距离为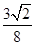 .(10分)
.(10分)
考点:1.参数方程与普通方程的互化;2.极坐标方程与直角坐标方程的互化;3.点到直线的距离公式;4.配方法求最值.


科目:高中数学 来源: 题型:解答题
在平面直角坐标系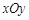 中,曲线
中,曲线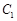 的参数方程为
的参数方程为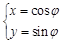 (
(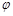 为参数),曲线
为参数),曲线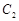 的参数方程为
的参数方程为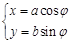 (
(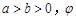 为参数).在以
为参数).在以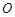 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线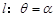 与
与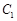 ,
,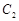 各有一个交点.当
各有一个交点.当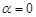 时,这两个交点间的距离为
时,这两个交点间的距离为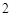 ,当
,当 时,这两个交点重合.
时,这两个交点重合.
(Ⅰ)分别说明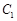 ,
,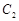 是什么曲线,并求出a与b的值;
是什么曲线,并求出a与b的值;
(Ⅱ)设当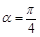 时,
时,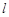 与
与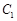 ,
,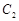 的交点分别为
的交点分别为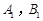 ,当
,当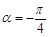 时,
时,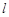 与
与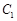 ,
,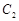 的交点分别为
的交点分别为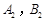 ,求四边形
,求四边形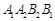 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题10分)选修4—4:坐标系与参数方程
已知曲线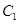 的参数方程为
的参数方程为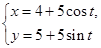 (
(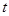 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,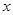 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线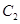 的极坐标方程为
的极坐标方程为 。
。
(Ⅰ)把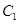 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(Ⅱ)求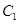 与
与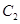 交点的极坐标(
交点的极坐标(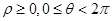 )。
)。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
极坐标系与直角坐标系 有相同的长度单位,以原点
有相同的长度单位,以原点 为极点,以
为极点,以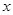 轴正半轴为极轴.已知直线
轴正半轴为极轴.已知直线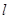 的参数方程为
的参数方程为 (
(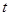 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线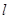 与曲线
与曲线 交于
交于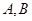 两点,求弦长
两点,求弦长 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的中年职工为5人,则样本容量为( )
| A.7 | B.15 | C.25 | D.35 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com