
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)求证:函数![]() 和
和![]() 在公共定义域内,
在公共定义域内,![]() 恒成立;
恒成立;
(3)若存在两个不同的实数![]() ,
,![]() ,满足
,满足![]() ,求证:
,求证:![]() .
.
【答案】(1)增区间为![]() ,减区间为
,减区间为![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】分析:(1)构造函数![]() ,对函数求导,得到得到导函数的正负,进而得到单调区间和极值;(2)构造函数
,对函数求导,得到得到导函数的正负,进而得到单调区间和极值;(2)构造函数![]() ,对函数
,对函数![]() 和
和![]() 求导研究函数的单调性进而得到函数的最值,使得最小值大于2即可;(3)要证原式只需要证
求导研究函数的单调性进而得到函数的最值,使得最小值大于2即可;(3)要证原式只需要证![]() ,
,![]() 故得到即证:
故得到即证:![]() ,变量集中设
,变量集中设![]() 即可,转化为关于t的不等式.
即可,转化为关于t的不等式.
详解:
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
故当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;
;
(2)证明:函数![]() 和
和![]() 的公共定义域为
的公共定义域为![]() ,
,
![]() ,
,
设![]() ,则
,则![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ;
;
设![]() ,当
,当![]() 时有极大值点,
时有极大值点,
![]() ;故
;故![]() ;
;
故函数![]() 和
和![]() 在公共定义域内,
在公共定义域内,![]() .
.
(3)证明:不妨设![]() ,由题意得,
,由题意得,
![]() ,
,![]() ;所以
;所以![]() ;
;
而要证![]() ,只需证明
,只需证明![]() ;
;
即证明![]() ;即证明
;即证明![]() ;
;
即证明, ;令
;令![]() ,则
,则![]() ;
;
即证明 ;设
;设![]() ;
;
则![]() ,故函数
,故函数![]() 在区间
在区间![]() 上是增函数,
上是增函数,
所以![]() ,即
,即![]() ;所以不等式
;所以不等式![]() 成立.
成立.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
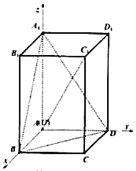
【题目】如图,在正四棱柱ABCD﹣A1B1C1D1中,AB=1,AA1=t,建立如图所示的空间直角坐标系O—xyz.
(1)若t=1,求异面直线AC1与A1B所成角的大小;
(2)若t=5,求直线AC1与平面A1BD所成角的正弦值;
(3)若二面角A1—BD—C的大小为120°,求实数t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
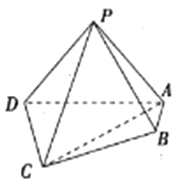
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为了解该商场某商品近5年日销售量(单位:件),随机抽取近5年50天的销售量,统计结果如下:
日销售量 | 100 | 150 |
天数 | 30 | 20 |
频率 |
|
|
若将上表中频率视为概率,且每天的销售量相互独立.则在这5年中:
(1)求5天中恰好有3天销售量为150件的概率(用分式表示);
(2)已知每件该商品的利润为20元,用X表示该商品某两天销售的利润和(单位: 元),求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始按如下规则依次取它的项:第一次取1;第二次取2个连续偶数![]() ;第三次取3个连续奇数
;第三次取3个连续奇数![]() ;第四次取4个连续偶数
;第四次取4个连续偶数![]() ;第五次取5个连续奇数
;第五次取5个连续奇数![]() ;……按此规律取下去,得到一个子数列
;……按此规律取下去,得到一个子数列![]() ,
,![]() ,……则在这个子数列中,第
,……则在这个子数列中,第![]() 个数是( )
个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系.若直线l的极坐标方程为 ![]() ,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 .
,曲线C的极坐标方程为:ρsin2θ=cosθ,将曲线C上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线C1 .
(Ⅰ)求曲线C1的直角坐标方程;
(Ⅱ)已知直线l与曲线C1交于A,B两点,点P(2,0),求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足acosC=b﹣ ![]() c. (Ⅰ)求角A的大小;
c. (Ⅰ)求角A的大小;
(Ⅱ)若B= ![]() ,AC=4,求BC边上的中线AM的长.
,AC=4,求BC边上的中线AM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车已成为一种时髦的新型环保交通工具,某共享单车公司为了拓展市场,对![]() ,
,![]() 两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
两个品牌的共享单车在编号分别为1,2,3,4,5的五个城市的用户人数(单位:十万)进行统计,得到数据如下:
城市品牌 | 1 | 2 | 3 | 4 | 5 |
| 3 | 4 | 12 | 6 | 8 |
| 4 | 3 | 7 | 9 | 5 |
(Ⅰ)若共享单车用户人数超过50万的城市称为“优城”,否则称为“非优城”,据此判断能否有![]() 的把握认为“优城”和共享单车品牌有关?
的把握认为“优城”和共享单车品牌有关?
(Ⅱ)若不考虑其它因素,为了拓展市场,对![]() 品牌要从这五个城市选择三个城市进行宣传.
品牌要从这五个城市选择三个城市进行宣传.
(i)求城市2被选中的概率;
(ii)求在城市2被选中的条件下城市3也被选中的概率.
附:参考公式及数据
| 0.15 | 0.10 | 0.05 | 0.025 | 0.005 | 0.001 | |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com