
【题目】已知数列![]() ,
,![]() ,且
,且![]() 对任意n
对任意n![]() 恒成立.
恒成立.
(1)求证:![]() (
(![]() );
);
(2)求证:![]() (
(![]() ).
).
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,已知PA,PB,PC两两垂直,PB=3,PC=4,且三棱锥P﹣ABC的体积为10.
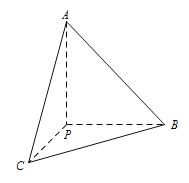
(1)求点A到直线BC的距离;
(2)若D是棱BC的中点,求异面直线PB,AD所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人经营淡水池塘养草鱼,根据过去![]() 期的养殖档案,该池塘的养殖重量
期的养殖档案,该池塘的养殖重量![]() (百斤)都在
(百斤)都在![]() 百斤以上,其中不足
百斤以上,其中不足![]() 百斤的
百斤的![]() 期,不低于
期,不低于![]() 百斤且不超过
百斤且不超过![]() 百斤的有
百斤的有![]() 期,超过
期,超过![]() 百斤的有
百斤的有![]() 期.根据统计,该池塘的草鱼重量的增加量
期.根据统计,该池塘的草鱼重量的增加量![]() (百斤)与使用某种饵料的质量
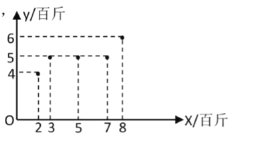
(百斤)与使用某种饵料的质量![]() (百斤)之间的关系如图所示.
(百斤)之间的关系如图所示.
鱼的重量(单位:百斤) |
|
|
|
冲水机运行台数 | 1 | 2 | 3 |
(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 关于
关于![]() 的回归方程
的回归方程![]() ;如果此人设想使用某种饵料
;如果此人设想使用某种饵料![]() 百斤时,草鱼重量的增加量须多于
百斤时,草鱼重量的增加量须多于![]() 百斤,请根据回归方程计算,确定此方案是否可行?并说明理由.
百斤,请根据回归方程计算,确定此方案是否可行?并说明理由.
(2)养鱼的池塘对水质含氧与新鲜度要求较高,故养殖户需设置若干台增氧冲水机,每期养殖使用的冲水机运行台数与鱼塘的鱼重量有关,并有如下关系:
若某台增氧冲水机运行,则该台冲水机每期盈利![]() 千元;若某台冲水机未运行,则该台冲水机每期亏损
千元;若某台冲水机未运行,则该台冲水机每期亏损![]() 千元.以频率 作为概率,养殖户欲使每期冲水机总利润的均值达到最大,应安装几台增氧冲水机?
千元.以频率 作为概率,养殖户欲使每期冲水机总利润的均值达到最大,应安装几台增氧冲水机?
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: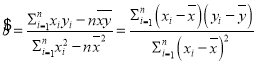 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,若曲线
,若曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左焦点为
的左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
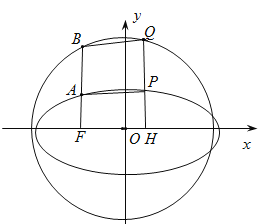
(1)求椭圆![]() 的方程;
的方程;
(2)已知圆![]() ,连接
,连接![]() 并延长交圆
并延长交圆![]() 于点
于点![]() 为椭圆长轴上一点(异于左、右焦点),过点
为椭圆长轴上一点(异于左、右焦点),过点![]() 作椭圆长轴的垂线分别交椭圆
作椭圆长轴的垂线分别交椭圆![]() 和圆
和圆![]() 于点
于点![]() (
(![]() 均在
均在![]() 轴上方).连接
轴上方).连接![]() ,记
,记![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() .
.
①求![]() 的值;
的值;
②求证:直线![]() 的交点在定直线上.
的交点在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商家统计了去年![]() ,
,![]() 两种产品的月销售额(单位:万元),绘制了月销售额的雷达图,图中
两种产品的月销售额(单位:万元),绘制了月销售额的雷达图,图中![]() 点表示
点表示![]() 产品2月份销售额约为20万元,
产品2月份销售额约为20万元,![]() 点表示
点表示![]() 产品9月份销售额约为25万元.
产品9月份销售额约为25万元.
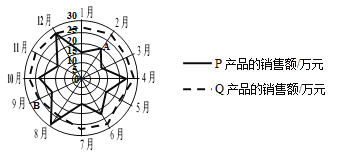
根据图中信息,下面统计结论错误的是( )
A.![]() 产品的销售额极差较大B.
产品的销售额极差较大B.![]() 产品销售额的中位数较大
产品销售额的中位数较大
C.![]() 产品的销售额平均值较大D.
产品的销售额平均值较大D.![]() 产品的销售额波动较小
产品的销售额波动较小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某区“创文明城区”![]() 简称“创城”
简称“创城”![]() 活动中,教委对本区A,B,C,D四所高中校按各校人数分层抽样调查,将调查情况进行整理后制成如表:
活动中,教委对本区A,B,C,D四所高中校按各校人数分层抽样调查,将调查情况进行整理后制成如表:
学校 | A | B | C | D |
抽查人数 | 50 | 15 | 10 | 25 |
“创城”活动中参与的人数 | 40 | 10 | 9 | 15 |
![]() 注:参与率是指:一所学校“创城”活动中参与的人数与被抽查人数的比值
注:参与率是指:一所学校“创城”活动中参与的人数与被抽查人数的比值![]()
假设每名高中学生是否参与“创城”活动是相互独立的.
![]() Ⅰ
Ⅰ![]() 若该区共2000名高中学生,估计A学校参与“创城”活动的人数;
若该区共2000名高中学生,估计A学校参与“创城”活动的人数;
![]() Ⅱ
Ⅱ![]() 在随机抽查的100名高中学生中,从A,C两学校抽出的高中学生中各随机抽取1名学生,求恰有1人参与“创城”活动的概率;
在随机抽查的100名高中学生中,从A,C两学校抽出的高中学生中各随机抽取1名学生,求恰有1人参与“创城”活动的概率;
![]() Ⅲ
Ⅲ![]() 若将表中的参与率视为概率,从A学校高中学生中随机抽取3人,求这3人参与“创城”活动人数的分布列及数学期望.
若将表中的参与率视为概率,从A学校高中学生中随机抽取3人,求这3人参与“创城”活动人数的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com