
【题目】如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(﹣ ![]() ,
, ![]() ),∠AOB=α.
),∠AOB=α. 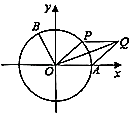
(1)求 ![]() 的值;
的值;
(2)设∠AOP=θ( ![]() ≤θ≤
≤θ≤ ![]() ),
), ![]() =
= ![]() +
+ ![]() ,四边形OAQP的面积为S,f(θ)=(
,四边形OAQP的面积为S,f(θ)=( ![]()
![]() ﹣
﹣ ![]() )2+2S2﹣
)2+2S2﹣ ![]() ,求f(θ)的最值及此时θ的值.
,求f(θ)的最值及此时θ的值.
【答案】
(1)解:依题意,tanα═﹣2,
∴ ![]() =
= ![]() =﹣
=﹣ ![]()
(2)解:由已知点P的坐标为P(cosθ,sinθ),
又 ![]() =
= ![]() +
+ ![]() ,|
,| ![]() =||
=|| ![]() |,
|,
∴四边形OAQP为菱形,
∴S=2S△OAP=sinθ,
∵A(1,0),P(cosθ,sinθ),
∴ ![]() =(1+cosθ,sinθ),
=(1+cosθ,sinθ),
∴ ![]()
![]() =1+cosθ,
=1+cosθ,
∴f(θ)=(cosθ+ ![]() )2+2sin2θ﹣
)2+2sin2θ﹣ ![]() =﹣(cosθ﹣
=﹣(cosθ﹣ ![]() )2+2
)2+2
∵﹣ ![]() ≤cosθ≤
≤cosθ≤ ![]() ,
,
∴当cosθ= ![]() ,即θ=
,即θ= ![]() 时,f(θ)max=2;
时,f(θ)max=2;
当cosθ=﹣ ![]() ,即θ=
,即θ= ![]() 时,f(θ)min=1
时,f(θ)min=1
【解析】(1)依题意,可求得tanα=﹣2,将 ![]() 中的“弦”化“切”即可求得其值;(2)利用向量的数量积的坐标运算可求得f(θ)=(cosθ+
中的“弦”化“切”即可求得其值;(2)利用向量的数量积的坐标运算可求得f(θ)=(cosθ+ ![]() )2+2sin2θ﹣
)2+2sin2θ﹣ ![]() =﹣(cosθ﹣
=﹣(cosθ﹣ ![]() )2+2,利用﹣
)2+2,利用﹣ ≤cosθ≤
![]() ,即可求得f(θ)的最值及此时θ的值.
,即可求得f(θ)的最值及此时θ的值.


科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,四边形ACFE是矩形,且平面ACFE⊥平面ABCD,点M在线段EF上. (I)求证:BC⊥平面ACFE;
(II)当EM为何值时,AM∥平面BDF?证明你的结论.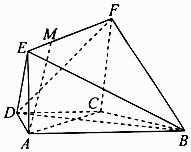
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,给出以下结论: ①直线A1B与B1C所成的角为60°;
②若M是线段AC1上的动点,则直线CM与平面BC1D所成角的正弦值的取值范围是 ![]() ;
;
③若P,Q是线段AC上的动点,且PQ=1,则四面体B1D1PQ的体积恒为 ![]() .
.
其中,正确结论的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2﹣(1+a)x+y2﹣ay+a=0(a∈R). (Ⅰ) 若a=1,求直线y=x被圆C所截得的弦长;
(Ⅱ) 若a>1,如图,圆C与x轴相交于两点M,N(点M在点N的左侧).过点M的动直线l与圆O:x2+y2=4相交于A,B两点.问:是否存在实数a,使得对任意的直线l均有∠ANM=∠BNM?若存在,求出实数a的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 为偶函数.
为偶函数.
(1)求实数t值;
(2)记集合E={y|y=f(x),x∈{1,2,3}},λ=lg22+lg2lg5+lg5﹣1,判断λ与E的关系;
(3)当x∈[a,b](a>0,b>0)时,若函数f(x)的值域为[2﹣ ![]() ,2﹣
,2﹣ ![]() ],求实数a,b的值.
],求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx﹣ ![]() )(
)( ![]() <ω<2),在区间(0,
<ω<2),在区间(0, ![]() )上( )
)上( )
A.既有最大值又有最小值
B.有最大值没有最小值
C.有最小值没有最大值
D.既没有最大值也没有最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=4sinx(cosx﹣sinx)+3 (Ⅰ)当x∈(0,π)时,求f(x)的单调递减区间;
(Ⅱ)若f(x)在[0,θ]上的值域为[0,2 ![]() +1],求cos2θ的值.
+1],求cos2θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=| ![]() ﹣ax|,若对任意的正实数a,总存在x0∈[1,4],使得f(x0)≥m,则实数m的取值范围为( )
﹣ax|,若对任意的正实数a,总存在x0∈[1,4],使得f(x0)≥m,则实数m的取值范围为( )
A.(﹣∞,0]
B.(﹣∞,1]
C.(﹣∞,2]
D.(﹣∞,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,a2=6,且数列{an﹣1﹣an}{n∈N*}是公差为2的等差数列.
(1)求{an}的通项公式;
(2)记数列{ ![]() }的前n项和为Sn , 求满足不等式Sn>
}的前n项和为Sn , 求满足不等式Sn> ![]() 的n的最小值.
的n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com