
【题目】在悠久灿烂的中国古代文化中,数学文化是其中的一朵绚丽的奇葩.《张丘建算经》是我国古代有标志性的内容丰富的众多数学名著之一,大约创作于公元五世纪.书中有如下问题:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈,问日益几何?”.其大意为:“有一女子擅长织布,织布的速度一天比一天快,从第二天起,每天比前一天多织相同数量的布,第一天织![]() 尺,一个月共织了九匹三丈,问从第二天起,每天比前一天多织多少尺布?”.已知
尺,一个月共织了九匹三丈,问从第二天起,每天比前一天多织多少尺布?”.已知![]() 匹
匹![]() 丈,
丈,![]() 丈
丈![]() 尺,若这一个月有
尺,若这一个月有![]() 天,记该女子这一个月中的第
天,记该女子这一个月中的第![]() 天所织布的尺数为
天所织布的尺数为![]() ,
,![]() ,对于数列
,对于数列![]() 、
、![]() ,下列选项中正确的为( )
,下列选项中正确的为( )
A.![]() B.
B.![]() 是等比数列C.
是等比数列C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】如图,设![]() 是椭圆
是椭圆![]() 的左焦点,直线:
的左焦点,直线:![]() 与
与![]() 轴交于
轴交于![]() 点,
点,![]() 为椭圆的长轴,已知
为椭圆的长轴,已知![]() ,且
,且![]() ,过
,过![]() 点作斜率为
点作斜率为![]() 直线
直线![]() 与椭圆相交于不同的两点
与椭圆相交于不同的两点![]() ,
,
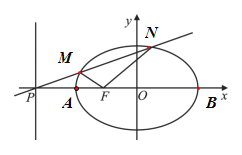
(1)当![]() 时,线段
时,线段![]() 的中点为
的中点为![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,求
,求![]() ;
;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在其图象上存在不同的两点
在其图象上存在不同的两点![]() ,其坐标满足条件:
,其坐标满足条件:![]() 的最大值为0,则称
的最大值为0,则称![]() 为“柯西函数”,则下列函数:
为“柯西函数”,则下列函数:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中是“柯西函数”的为( )
.其中是“柯西函数”的为( )
A.①②B.③④C.①③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点为坐标原点O,对称轴为![]() 轴,其准线为
轴,其准线为![]() .
.
(1)求抛物线C的方程;
(2)设直线![]() ,对任意的
,对任意的![]() 抛物线C上都存在四个点到直线l的距离为
抛物线C上都存在四个点到直线l的距离为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,角A,B,C的对边分别为a,b,c,
中,角A,B,C的对边分别为a,b,c,![]()
(1)若![]() 还同时满足下列四个条件中的三个:①
还同时满足下列四个条件中的三个:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 的面积
的面积![]() ,请指出这三个条件,并说明理由;
,请指出这三个条件,并说明理由;
(2)若![]() ,求
,求![]() 周长L的取值范围.
周长L的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有两家共享单车公司,在市场上分别投放了黄、蓝两种颜色的单车,已知黄、蓝两种颜色的单车的投放比例为2:1.监管部门为了了解两种颜色的单车的质量,决定从市场中随机抽取5辆单车进行体验,若每辆单车被抽取的可能性相同.
(1)求抽取的5辆单车中有2辆是蓝色颜色单车的概率;
(2)在骑行体验过程中,发现蓝色单车存在一定质量问题,监管部门决定从市场中随机地抽取一辆送技术部门作进一步抽样检测,并规定若抽到的是蓝色单车,则抽样结束,若抽取的是黄色单车,则将其放回市场中,并继续从市场中随机地抽取下一辆单车,并规定抽样的次数最多不超过![]() (
(![]() )次.在抽样结束时,已取到的黄色单车以
)次.在抽样结束时,已取到的黄色单车以![]() 表示,求
表示,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为常数,函数
为常数,函数![]() 和
和![]() 的图象在它们与坐标轴交点处的切线互相平行.
的图象在它们与坐标轴交点处的切线互相平行.
(1)求![]() 的值;
的值;
(2)若存在![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)令![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为其右焦点,点
为其右焦点,点![]() 满足
满足![]() .
.
①证明: ![]() 为定值;
为定值;
②设直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() 成等差数列,求
成等差数列,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com