
【题目】2020年春季受新冠肺炎疫情的影响,利用网络软件办公与学习成为了一种新的生活方式,网上办公软件的开发与使用成为了一个热门话题.为了解“钉钉”软件的使用情况,“钉钉”公司借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
35岁及以下 | 70 | 30 | 100 |
35岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为“钉钉”软件的使用情况与年龄有关?
(2)现从所抽取的35岁以上的网友中利用分层抽样的方法再抽取5人.从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用“钉钉”软件的概率.
参考公式: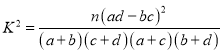 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)能在犯错误的概率不超过0.15的前提下认为“钉钉”软件的使用情况与年龄有关.
(2)![]()
【解析】
(1)根据列联表计算![]() ,再比较参考数据即可得到答案.
,再比较参考数据即可得到答案.
(2)首先利用分层抽样得到经常使用“钉钉”软件和偶尔或不用“钉钉”软件的人数,再利用古典概型公式即可得到答案.
(1)由列联表可得:![]() .
.
所以能在犯错误的概率不超过0.15的前提下认为“钉钉”软件的使用情况与年龄有关.
(2)依题意可得,在每层中所抽取的比例为![]() ,
,
所以从经常使用“钉钉”软件的人中抽取![]() (人),
(人),
从偶尔或不用“钉钉”软件的人中抽取![]() (人).
(人).
设这5人中,经常使用“钉钉”软件的3人分别为![]() ,
,![]() ,
,![]() ;
;
偶尔或不用“钉钉”软件的2人分别为![]() ,
,![]() ,
,
则从5人中选出2人的所有可能结果为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10种.
,共10种.
选出的2人中没有1人经常使用“钉钉”软件的可能结果为![]() ,共1种.
,共1种.
故选出的2人中至少有1人经常使用“钉钉”软件的概率![]() .
.


科目:高中数学 来源: 题型:
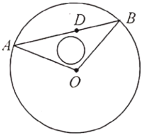
【题目】有一块以点![]() 为圆心,半径为
为圆心,半径为![]() 百米的圆形草坪,草坪内距离
百米的圆形草坪,草坪内距离![]() 点
点![]() 百米的
百米的![]() 点有一用于灌溉的水笼头,现准备过点
点有一用于灌溉的水笼头,现准备过点![]() 修一条笔直小路交草坪圆周于
修一条笔直小路交草坪圆周于![]() 两点,为了方便居民散步,同时修建小路
两点,为了方便居民散步,同时修建小路![]() ,其中小路的宽度忽略不计.
,其中小路的宽度忽略不计.
(1)若要使修建的小路的费用最省,试求小路的最短长度;
(2)若要在![]() 区域内(含边界)规划出一块圆形的场地用于老年人跳广场舞,试求这块圆形广场的最大面积.(结果保留根号和
区域内(含边界)规划出一块圆形的场地用于老年人跳广场舞,试求这块圆形广场的最大面积.(结果保留根号和![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念越来越深入人心,据此,某网站调查了人们对生态文明建设的关注情况,调查数据表明,参与调查的人员中关注生态文明建设的约占80%.现从参与调查的关注生态文明建设的人员中随机选出200人,并将这200人按年龄(单位:岁)分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65],得到的频率分布直方图如图所示.
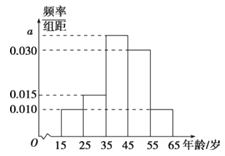
(Ⅰ)求这200人的平均年龄(每一组用该组区间的中点值作为代表)和年龄的中位数(保留一位小数);
(Ⅱ)现在要从年龄在第1,2组的人员中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求抽取的3人中恰有2人的年龄在第2组中的概率;
(Ⅲ)若从所有参与调查的人(人数很多)中任意选出3人,设这3人中关注生态文明建设的人数为X,求随机变量X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 的两个焦点,过
的两个焦点,过![]() ,
,![]() 分别作直线
分别作直线![]() ,
,![]() ,且
,且![]() ,若
,若![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 在
在![]() 轴上方),则四边形
轴上方),则四边形![]() 面积的最大值为__________.
面积的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某企业中随机抽取了5名员工测试他们的艺术爱好指数![]() 和创新灵感指数
和创新灵感指数![]() ,统计结果如下表(注:指数值越高素质越优秀):
,统计结果如下表(注:指数值越高素质越优秀):
![]()
(1)求创新灵感指数![]() 关于艺术爱好指数
关于艺术爱好指数![]() 的线性回归方程;
的线性回归方程;
(2)企业为提高员工的艺术爱好指数,要求员工选择音乐和绘画中的一种进行培训,培训音乐次数![]() 对艺术爱好指数
对艺术爱好指数![]() 的提高量为
的提高量为 ,培训绘画次数
,培训绘画次数![]() 对艺术爱好指数
对艺术爱好指数![]() 的提高量为
的提高量为![]() ,其中
,其中![]() 为参加培训的某员工已达到的艺术爱好指数.艺术爱好指数已达到3的员工甲选择参加音乐培训,艺术爱好指数已达到4的员工乙选择参加绘画培训,在他们都培训了20次后,估计谁的创新灵感指数更高?
为参加培训的某员工已达到的艺术爱好指数.艺术爱好指数已达到3的员工甲选择参加音乐培训,艺术爱好指数已达到4的员工乙选择参加绘画培训,在他们都培训了20次后,估计谁的创新灵感指数更高?
参考公式:回归方程![]() 中,
中, ,
,![]() .
.
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学经典《数书九章》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称为“阳马”,将四个面都为直角三角形的四面体称之为“鳖臑”.在如图所示的阳马![]() 中,底面ABCD是矩形.
中,底面ABCD是矩形.![]() 平面
平面![]() ,
,![]() ,
,![]() ,以
,以![]() 的中点O为球心,AC为直径的球面交PD于M(异于点D),交PC于N(异于点C).
的中点O为球心,AC为直径的球面交PD于M(异于点D),交PC于N(异于点C).
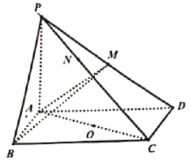
(1)证明:![]() 平面
平面![]() ,并判断四面体MCDA是否是鳖臑,若是,写出它每个面的直角(只需写出结论);若不是,请说明理由;
,并判断四面体MCDA是否是鳖臑,若是,写出它每个面的直角(只需写出结论);若不是,请说明理由;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F,直线l与C交于M,N两点.
的右焦点为F,直线l与C交于M,N两点.
(1)若l过点F,点M,N到直线y=2的距离分别为d1,d2,且![]() ,求l的方程;
,求l的方程;
(2)若点M的坐标为(0,1),直线m过点M交C于另一点N′,当直线l与m的斜率之和为2时,证明:直线NN′过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,右焦点为
的长轴长为4,右焦点为![]() ,且椭圆
,且椭圆![]() 上的点到点
上的点到点![]() 的距离的最小值与最大值的积为1,圆
的距离的最小值与最大值的积为1,圆![]() 与
与![]() 轴交于
轴交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且直线
两点,且直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的面积与
的面积与![]() 的面积乘积的取值范围.
的面积乘积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②若函数![]() 在
在![]() 上有两个零点,则
上有两个零点,则![]() 的取值范围是
的取值范围是![]() ;
;
③当![]() 时,函数
时,函数![]() 的最大值为0;
的最大值为0;
④函数![]() 在
在![]() 上单调递减;
上单调递减;
上述命题正确的是_________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com