
【题目】已知函数![]() (
(![]() ,
,![]() )的图象的相邻两条对称轴之间的距离为4,且有一个零点为
)的图象的相邻两条对称轴之间的距离为4,且有一个零点为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新能源汽车包括纯电动汽车、增程式电动汽车、混合动力汽车、燃料电池电动汽车、氢发动机汽车、其他新能源汽车等.它是未来汽车的发展方向.一个新能源汽车制造厂引进了一条新能源汽车整车装配流水线,这条流水线生产的新能源汽车数量![]() (辆)与创造的价值
(辆)与创造的价值![]() (万元)之间满足二次函数关系.已知产量为0时,创造的价值也为0;当产量为40000辆时,创造的价值达到最大6000万元.若这家工厂希望利用这条流水线创收达到5625万元,则它可能生产的新能源汽车数量是___________辆.
(万元)之间满足二次函数关系.已知产量为0时,创造的价值也为0;当产量为40000辆时,创造的价值达到最大6000万元.若这家工厂希望利用这条流水线创收达到5625万元,则它可能生产的新能源汽车数量是___________辆.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中万事万物都是有关联的,所有直线中有关联直线,所有点中也有相关点,现在定义:平面内如果两点![]() 、
、![]() 都在函数
都在函数![]() 的图像上,而且满足
的图像上,而且满足![]() 、
、![]() 两点关于原点对称,则称点对(
两点关于原点对称,则称点对(![]() 、
、![]() )是函数
)是函数![]() 的“相关对称点对”(注明:点对(
的“相关对称点对”(注明:点对(![]() 、
、![]() )与(
)与(![]() 、
、![]() )看成同一个“相关对称点对”).已知函数
)看成同一个“相关对称点对”).已知函数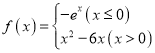 ,则这个函数的“相关对称点对”有( )
,则这个函数的“相关对称点对”有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
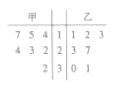
【题目】某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示.
(1)求甲、乙两名运动员得分的中位数;
(2)你认为哪位运动员的成绩更稳定?
(3)如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分,求甲的得分大于乙的得分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com