
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为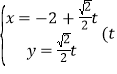 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
【答案】(1)4;(2)16.
【解析】
(1)根据题意,将曲线C的极坐标方程变形为标准方程,将直线的参数方程与曲线C的方程联立,可得![]() ,由一元二次方程根与系数的关系计算可得答案;
,由一元二次方程根与系数的关系计算可得答案;
(2)写出曲线C的参数方程,分析可得以P为顶点的内接矩形周长l![]() ,由正弦函数的性质分析可得答案.
,由正弦函数的性质分析可得答案.
(1)由![]() ,将x=ρcosθ,y=ρsinθ代入得到
,将x=ρcosθ,y=ρsinθ代入得到![]() +3
+3![]() =12,
=12,
所以曲线C的直角坐标方程为![]() +3
+3![]() =12,
=12,![]() 的极坐标为
的极坐标为![]() ,化为直角坐标为(-2,0)
,化为直角坐标为(-2,0)
由直线l的参数方程为: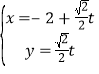 (t为参数),
(t为参数),
知直线l是过点P(-2,0),且倾斜角为![]() 的直线,
的直线,
把直线的参数方程代入曲线C得,![]() .
.
所以|PM||PN|=|t1t2|=4.
(2)由曲线C的方程为 ![]() ,
,
不妨设曲线C上的动点![]() ,
,
则以P为顶点的内接矩形周长l![]() ,
,
又由sin(θ![]() )≤1,则l≤16;
)≤1,则l≤16;
因此该内接矩形周长的最大值为16.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某地统计局调查了10000名居民的月收入,并根据所得数据绘制了样本的频率分布直方图如图所示。
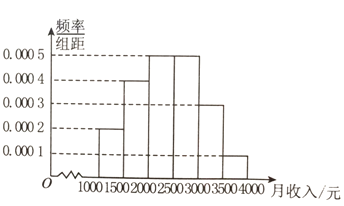
(1)求居民月收入在[3000,3500)内的频率;
(2)根据频率分布直方图求出样本数据的中位数;
(3)为了分析居民的月收入与年龄、职业等方面的关系,必须按月收入再从这10000中用分层抽样的方法抽出100人做进一步分析,则应从月收入在[2500,3000)内的居民中抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年我国全面建成小康社会,其中小康生活的住房标准是城镇人均住房建筑面积30平方米. 下表为2007年—2016年中,我区城镇和农村人均住房建筑面积统计数据. 单位:平方米.
2007年 | 2008年 | 2009年 | 2010年 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
城镇 | 18.66 | 20.25 | 22.79 | 25 | 27.1 | 28.3 | 31.6 | 32.9 | 34.6 | 36.6 |
农村 | 23.3 | 24.8 | 26.5 | 27.9 | 30.7 | 32.4 | 34.1 | 37.1 | 41.4 | 45.8 |
(1)现从上述表格中随机抽取一年数据,试估计该年城镇人均住房建筑面积达到小康生活住房标准的概率;
(2)现从上述表格中随机抽取连续两年数据,求这两年中城镇人均住房建筑面积增长不少于2平方米的概率;
(3)将城镇和农村的人均住房建筑面积经四舍五入取整后作为样本数据.记2012—2016年中城镇人均住房面积的方差为![]() ,农村人均住房面积的方差为
,农村人均住房面积的方差为![]() ,判断
,判断![]() 与
与![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
(注:方差![]() ,其中
,其中![]() 为
为 ![]()
![]() ,……
,…… ![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
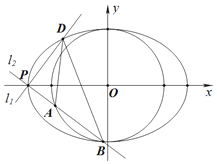
【题目】如图,已知![]() 是椭圆
是椭圆![]() 的一个顶点,
的一个顶点,![]() 的短轴是圆
的短轴是圆![]() 的直径,直线
的直径,直线![]() ,
,![]() 过点P且互相垂直,
过点P且互相垂直,![]() 交椭圆
交椭圆![]() 于另一点D,
于另一点D,![]() 交圆
交圆![]() 于A,B两点
于A,B两点
![]() Ⅰ
Ⅰ![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() Ⅱ
Ⅱ![]() 求
求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】央视传媒为了解央视举办的“朗读者”节目的收视时间情况,随机抽取了某市名![]() 观众进行调查,其中有
观众进行调查,其中有![]() 名男观众和
名男观众和![]() 名女观众,将这
名女观众,将这![]() 名观众收视时间编成如图所示的茎叶图(单位:分钟),收视时间在
名观众收视时间编成如图所示的茎叶图(单位:分钟),收视时间在![]() 分钟以上(包括
分钟以上(包括![]() 分钟)的称为“朗读爱好者”,收视时间在
分钟)的称为“朗读爱好者”,收视时间在![]() 分钟以下(不包括
分钟以下(不包括![]() 分钟)的称为“非朗读爱好者”.
分钟)的称为“非朗读爱好者”.

(1)若采用分层抽样的方法从“朗读爱好者”和“非朗读爱好者”中随机抽取![]() 名,再从这
名,再从这![]() 名观众中任选
名观众中任选![]() 名,求至少选到
名,求至少选到![]() 名“朗读爱好者”的概率;
名“朗读爱好者”的概率;
(2)若从收视时间在40分钟以上(包括40分钟)的所有观众中选出男、女观众各1名,求选出的这两名观众时间相差5分钟以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以椭圆![]() 的焦点和短轴端点为顶点的四边形恰好是面积为4的正方形.
的焦点和短轴端点为顶点的四边形恰好是面积为4的正方形.
(1)求椭圆![]() 的方程:
的方程:
(2)若![]() 是椭圆
是椭圆![]() 上的动点,求
上的动点,求![]() 的取值范围;
的取值范围;
(3)直线![]() :
:![]() 与椭圆
与椭圆![]() 交于异于椭圆顶点的
交于异于椭圆顶点的![]() ,
,![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() 点,直线
点,直线![]() 和直线
和直线![]() 的斜率之积为1,直线
的斜率之积为1,直线![]() 与
与![]() 轴交于点
轴交于点![]() .若直线
.若直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() 试判断
试判断![]() ,是否为定值,若是,求出该定值;若不是,说明理由.
,是否为定值,若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com