
【题目】如图,四棱锥A﹣BCDE中,AB、BC、BE两两垂直且AB=BC=BE,DE∥BC,DE=2BC,F是AE的中点.
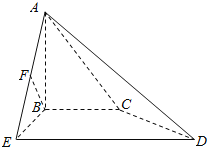
(1)求证:BF∥面ACD;
(2)求证:面ADE⊥面ACD.
【答案】(1)见解析(2)见解析
【解析】
(1)取AD的中点M,连接CM、MF,推导出四边形BCMF为平行四边形,从而CM∥BF,由此能证明BF∥面ACD.
(2)作DE中点N,连接CN,推导出CM⊥AD,BF⊥AE,CM⊥AE,由此能证明面ADE⊥面ACD.
证明:(1)取AD的中点M,连接CM、MF.
∵F、M分别为AE、AD中点,∴DE∥2MF,DE=2MF
又∵DE∥2BC,DE=2BC∴FM∥BC,FM=BC,
∴四边形BCMF为平行四边形,∴CM∥BF,
又∵BF面ACD,CM面ACD,
∴BF∥面ACD.
(2)作DE中点N,连接CN,
∵DE∥2BC,DE=2BC,N为DE中点N,∴DN=BC,
又∵AB、BC、BE两两垂直,且AB=BC=BE,∴AC=CD,
∵M为AD中点,∴CM⊥AD,
又∵F是AE的中点,且AB=BE,∴BF⊥AE,
∵CM∥BF,∴CM⊥AE,
又∵AD∩AE=A,AE、AD面ADE,∴CM⊥面ADE,
∵CM面ACD,∴面ADE⊥面ACD.



科目:高中数学 来源: 题型:
【题目】2020年寒假,因为“新冠”疫情全体学生只能在家进行网上学习,为了研究学生网上学习的情况,某学校随机抽取![]() 名学生对线上教学进行调查,其中男生与女生的人数之比为
名学生对线上教学进行调查,其中男生与女生的人数之比为![]() ,抽取的学生中男生有
,抽取的学生中男生有![]() 人对线上教学满意,女生中有
人对线上教学满意,女生中有![]() 名表示对线上教学不满意.
名表示对线上教学不满意.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对线上教学是否满意 与性别有关”;
的把握认为“对线上教学是否满意 与性别有关”;
态度 性别 | 满意 | 不满意 | 合计 |
男生 | |||
女生 | |||
合计 | 100 |
(2)从被调查的对线上教学满意的学生中,利用分层抽样抽取![]() 名学生,再在这
名学生,再在这![]() 名学生中抽取
名学生中抽取![]() 名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
名学生,作线上学习的经验介绍,求其中抽取一名男生与一名女生的概率.
附: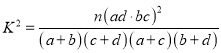 .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于![]() ,直线l与椭圆C交于
,直线l与椭圆C交于![]() 两点,其中直线l不过原点.
两点,其中直线l不过原点.
(1)求椭圆C的方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,其中
,其中![]() 且
且![]() .记
.记![]() 的面积为S.分别以
的面积为S.分别以![]() 为直径的圆的面积依次为
为直径的圆的面积依次为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,∠ACB=90°,∠ABC=45°,AB=AA1=2,P为CC1的中点.
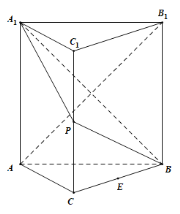
(1)证明:AB1⊥平面PA1B;
(2)设E为BC的中点,线段AB1上是否存在一点Q,使得QE∥平面A1ACC1?若存在,求四棱锥Q﹣AA1C1C的体积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成.
(1)求出甲考生正确完成题数的概率分布列,并计算数学期望;
(2)若考生乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响.试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
,且每题正确完成与否互不影响.试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)问:![]() 的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在极坐标系![]() 中,
中,![]() ,
,![]() ,弧
,弧![]() ,
,![]() ,
,![]() 所在圆的圆心分别为
所在圆的圆心分别为![]() ,
,![]() ,
,![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() .
.
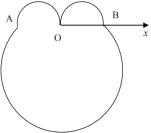
(1)写出曲线![]() ,
,![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 由
由![]() ,
,![]() ,
,![]() 构成,若曲线
构成,若曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() ),写出曲线
),写出曲线![]() 与曲线
与曲线![]() 的所有公共点(除极点外)的极坐标.
的所有公共点(除极点外)的极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com