
 ,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.
,AB=8,BC=6,点E是PC的中点,F在AD上且AF:FD=1:2.建立适当坐标系.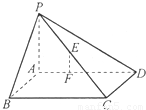
 ,
, ,
, 分别为x,y,z轴建立直角坐标系,根据已知条件求出F,P,C,E点的坐标,利用两点间距离公式即可求得EF长;
分别为x,y,z轴建立直角坐标系,根据已知条件求出F,P,C,E点的坐标,利用两点间距离公式即可求得EF长; ,
, 的坐标,只需证明
的坐标,只需证明 =0;
=0; 解:(1)以A为原点,
解:(1)以A为原点, ,
, ,
, 分别为x,y,z轴建立直角坐标系,
分别为x,y,z轴建立直角坐标系, ),C(8,6,0),从而E(4,3,
),C(8,6,0),从而E(4,3, ),
), =6.
=6. =(-4,-1,-
=(-4,-1,- ),
), =(8,6,-2
=(8,6,-2 ),
), =-4×8+(-1)×6+(-
=-4×8+(-1)×6+(- )×(-2
)×(-2 )=0,
)=0,

科目:高中数学 来源: 题型:
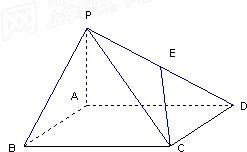 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点查看答案和解析>>
科目:高中数学 来源: 题型:
 (理)如图,四棱锥P-ABCD的底面是矩形,PA⊥面ABCD,PA=2
(理)如图,四棱锥P-ABCD的底面是矩形,PA⊥面ABCD,PA=2| 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年龙岩一中冲刺理)(12分)
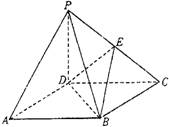
如图,四棱锥P―ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)证明PA//平面BDE;
(2)求二面角B―DE―C的大小;
(3)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年惠州一中三模理) 如图,四棱锥P―ABCD的底面是AB=2,BC=![]() 的矩形,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD
的矩形,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD
(I)证明:侧面PAB⊥侧面PBC;
(II)求侧棱PC与底面ABCD所成的角;
(III)求直线AB与平面PCD的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com