
【题目】已知O为坐标原点,抛物线C:y2=8x上一点A到焦点F的距离为6,若点P为抛物线C准线上的动点,则|OP|+|AP|的最小值为( )
A. 4B. ![]() C.
C. ![]() D.
D. ![]()
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,顶点
为菱形,顶点![]() 在底面
在底面![]() 的射影恰好是菱形
的射影恰好是菱形![]() 对角线的交点
对角线的交点![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() .
.
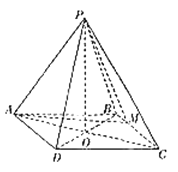
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018年10月考考试中,成都外国语学校共有250名高三文科学生参加考试,数学成绩的频率分布直方图如图:
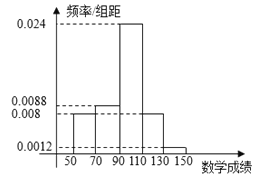
(1)如果成绩大于130的为特别优秀,这250名学生中本次考试数学成绩特别优秀的大约多少人?
(2)如果这次考试语文特别优秀的有5人,语文和数学两科都特别优秀的共有2人,从(1)中的数学成绩特别优秀的人中随机抽取2人,求选出的2人中恰有1名两科都特别优秀的概率.
(3)根据(1),(2)的数据,是否有99%以上的把握认为语文特别优秀的同学,数学也特别优秀?
①![]()
②
P( | 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园举办“yue”主题系列活动——“悦”动越健康亲子运动打卡活动,为了解小朋友坚持打卡的情况,对该幼儿园所有小朋友进行了调查,调查结果如下表:
打卡天数 | 17 | 18 | 19 | 20 | 21 |
男生人数 | 3 | 5 | 3 | 7 | 2 |
女生人数 | 3 | 5 | 5 | 7 | 3 |
(1)根据上表数据,求该幼儿园男生平均打卡的天数;
(2)若从打卡21天的小朋友中任选2人交流心得,求选到男生和女生各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)已知动直线![]() 与圆
与圆![]() :
:![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点.是否存在实数
两点.是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 满足
满足![]() ,
,![]() ,
,![]() 为非零常数.
为非零常数.
(1)是否存在实数![]() ,使得数列
,使得数列![]() 成为等差数列或等比数列,若存在,找出所有的
成为等差数列或等比数列,若存在,找出所有的![]() ,及对应的通项公式;若不存在,说明理由;
,及对应的通项公式;若不存在,说明理由;
(2)当![]() 时,记
时,记![]() ,证明:数列
,证明:数列![]() 是等比数列;
是等比数列;
(3)求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 上任意一点到其焦点的距离的最小值为1.
上任意一点到其焦点的距离的最小值为1.![]() ,
,![]() 为抛物线上的两动点(
为抛物线上的两动点(![]() 、
、![]() 不重合且均异于原点),
不重合且均异于原点),![]() 为坐标原点,直线
为坐标原点,直线![]() 、
、![]() 的倾斜角分别为
的倾斜角分别为![]() ,
,![]() .
.
(1)求抛物线方程;
(2)若![]() ,求证直线
,求证直线![]() 过定点;
过定点;
(3)若![]() (
(![]() 为定值),探求直线
为定值),探求直线![]() 是否过定点,并说明理由.
是否过定点,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com