
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() :
:![]() .设圆
.设圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆心![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
【答案】(1) ![]() 或
或![]() . (2)
. (2) ![]()
【解析】
(1)先求出圆心坐标,可得圆的方程,再设出切线方程,利用点到直线的距离公式,即可求得切线方程;(2)设出点C,M的坐标,利用![]() ,根据点点距离的公式,寻找坐标之间的关系,进一步将问题转化为圆与圆的位置关系,即可得出结论.
,根据点点距离的公式,寻找坐标之间的关系,进一步将问题转化为圆与圆的位置关系,即可得出结论.
(1)由题设,圆心![]() 是直线
是直线![]() 和
和![]() 的交点,解得点
的交点,解得点![]() ,于是切线的斜率必存在.设过
,于是切线的斜率必存在.设过![]() 的圆
的圆![]() 的切线方程为
的切线方程为![]() ,
,
由题意,得![]() ,
,
解得![]() 或
或![]() ,
,
故所求切线方程为![]() 或
或![]() .
.
(2)因为圆心在直线![]() 上,
上,
所以圆![]() 的方程为
的方程为![]() .
.
设点![]() ,因为
,因为![]() ,
,
所以![]() ,
,
化简得![]() ,即
,即![]() ,
,
所以点![]() 在以
在以![]() 为圆心,2为半径的圆上.
为圆心,2为半径的圆上.
由题意,点![]() 在圆
在圆![]() 上,所以圆
上,所以圆![]() 与圆
与圆![]() 有公共点,则
有公共点,则![]() ,
,
即![]() .
.
整理,得![]() .
.
由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() .
.
所以点![]() 的横坐标
的横坐标![]() 的取值范围为
的取值范围为![]() .
.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x 的焦点为F.
(1)点A,P满足 ![]() .当点A在抛物线C上运动时,求动点P的轨迹方程;
.当点A在抛物线C上运动时,求动点P的轨迹方程;
(2)在x轴上是否存在点Q,使得点Q关于直线y=2x的对称点在抛物线C上?如果存在,求所有满足条件的点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】养路处建造圆锥形无底仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12m,高4m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4m(高不变);二是高度增加4m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组一次为[20,40),[40,60),[60,80),[80,100).若低于60分的人数是15人,则该班的学生人数是( ) 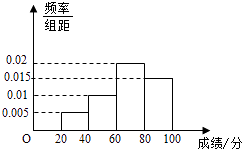
A.45
B.50
C.55
D.60
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)满足x2f′(x)+2xf(x)= ![]() ,f(2)=
,f(2)= ![]() ,则x>0时,f(x)( )
,则x>0时,f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线C1:x2=4y,C2:x2=﹣2py(p>0),点M(x0 , y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x0=1﹣ ![]() 时,切线MA的斜率为﹣
时,切线MA的斜率为﹣ ![]() .
. 
(1)求P的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的是__________.
①将一组数据中的每个数据都加上或减去同一个常数后,方差不变;
②在吸烟与患肺病这两个分类变量的独立性检验中,“有99%的把握认为吸烟与患肺病有关”的含义是“若某人吸烟,则他有99%的可能患肺病;”
③已知“![]() ”为真命题,则“
”为真命题,则“![]() ”、“
”、“![]() ”、“
”、“![]() ”中至少有一个真命题;
”中至少有一个真命题;
④以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,其变换后得到线性回归方程
,其变换后得到线性回归方程![]() 则
则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com