
如图,在五面体 中,已知
中,已知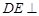 平面
平面 ,
,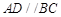 ,
,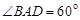 ,
,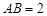 ,
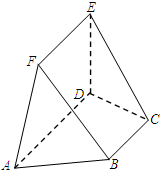
,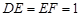 .
.
(1)求证: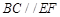 ;
;
(2)求三棱锥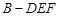 的体积.
的体积.
(1)详见解析,(2)
解析试题分析:(1)证明线线平行,一般思路为利用线面平行的性质定理与判定定理进行转化. 因为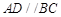 ,
,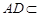 平面
平面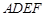 ,
,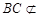 平面
平面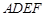 ,所以
,所以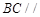 平面
平面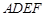 ,又
,又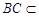 平面
平面 ,平面
,平面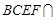 平面
平面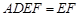 ,所以
,所以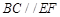 .(2)求三棱锥的体积,关键是找寻高.可由面面垂直性质定理探求,因为
.(2)求三棱锥的体积,关键是找寻高.可由面面垂直性质定理探求,因为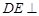 平面
平面 ,所以有面
,所以有面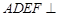 平面
平面 ,则作
,则作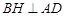 就可得
就可得 平面
平面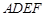 .证明
.证明 平面
平面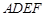 过程也可从线线垂直证线面垂直.确定
过程也可从线线垂直证线面垂直.确定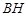 是三棱锥
是三棱锥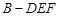 的高之后,可利用三棱锥
的高之后,可利用三棱锥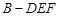 的体积公式
的体积公式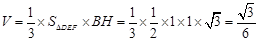 .
.
试题解析: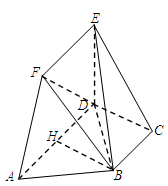
(1)因为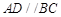 ,
,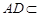 平面
平面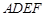 ,
,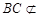 平面
平面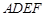 ,
,
所以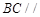 平面
平面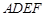 , 3分
, 3分
又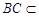 平面
平面 ,平面
,平面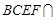 平面
平面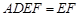 ,
,
所以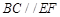 . 6分
. 6分
(2)在平面 内作
内作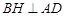 于点
于点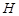 ,
,
因为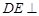 平面
平面 ,
,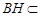 平面
平面 ,所以
,所以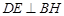 ,
,
又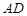 ,
,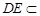 平面
平面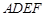 ,
,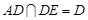 ,
,
所以 平面
平面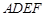 ,
,
所以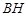 是三棱锥
是三棱锥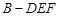 的高. 9分
的高. 9分
在直角三角形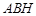 中,
中,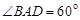 ,
,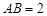 ,所以
,所以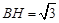 ,
,
因为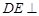 平面
平面 ,
,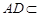 平面
平面 ,所以
,所以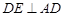 ,
,
又由(1)知,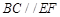 ,且
,且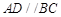 ,所以
,所以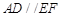


科目:高中数学 来源: 题型:解答题
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2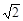 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.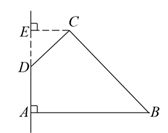
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知平面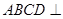 平面
平面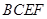 ,且四边形
,且四边形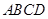 为矩形,四边形
为矩形,四边形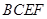 为直角梯形,
为直角梯形,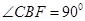 ,
,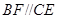 ,
,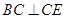 ,
,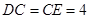 ,
,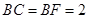 .
.
(1)作出这个几何体的三视图(不要求写作法).
(2)设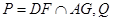 是直线
是直线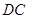 上的动点,判断并证明直线
上的动点,判断并证明直线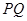 与直线
与直线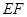 的位置关系.
的位置关系.
(3)求直线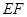 与平面
与平面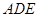 所成角的余弦值.
所成角的余弦值.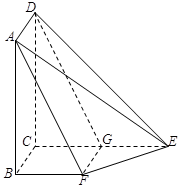
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•浙江)如图,在四面体A﹣BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2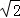 .M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
(1)证明:PQ∥平面BCD;
(2)若二面角C﹣BM﹣D的大小为60°,求∠BDC的大小.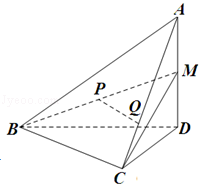
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点,△AEC面积的最小值是3.
(1)求证:AC⊥DE;
(2)求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一个几何体的三视图如图所示.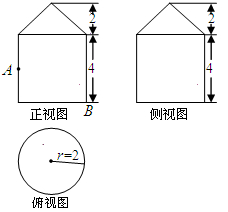
(1)求此几何体的表面积;
(2)在如图的正视图中,如果点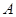 为所在线段中点,点
为所在线段中点,点 为顶点,求在几何体侧面上从点
为顶点,求在几何体侧面上从点 到点
到点 的最短路径的长.
的最短路径的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,矩形ABCD中,AB=a,AD=b,过点D作DE⊥AC于E,交直线AB于F.现将△ACD沿对角线AC折起到△PAC的位置,使二面角P AC
AC B的大小为60°.过P作PH⊥EF于H.
B的大小为60°.过P作PH⊥EF于H.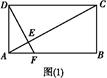
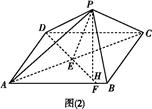
(1)求证:PH⊥平面ABC;
(2)若a+b=2,求四面体P ABC体积的最大值.
ABC体积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com