
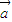 ∈M,都有
∈M,都有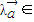 M,则称M为“点射域”,在此基础上给出下列四个向量集合:①{(x,y)|y≥x2};②{(x,y)|
M,则称M为“点射域”,在此基础上给出下列四个向量集合:①{(x,y)|y≥x2};②{(x,y)|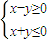 };③{(x,y)|x2+y2-2y≥0};④{(x,y)|3x2+2y2-12<0}.其中平面向量的集合为“点射域”的序号是 .
};③{(x,y)|x2+y2-2y≥0};④{(x,y)|3x2+2y2-12<0}.其中平面向量的集合为“点射域”的序号是 . 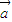 ∈M时,与它共线的向量
∈M时,与它共线的向量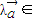 M也成立,
M也成立,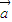 =(1,1)∈M,但3
=(1,1)∈M,但3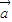 =(3,3)∉M,故它不是“点射域”;
=(3,3)∉M,故它不是“点射域”;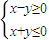 },可得任意正实数λ和向量
},可得任意正实数λ和向量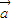 ∈M,都有
∈M,都有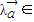 M,故它是“点射域”;
M,故它是“点射域”;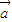 =(0,2)∈M,但
=(0,2)∈M,但
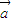 =(0,1)∉M,故它不是“点射域”;
=(0,1)∉M,故它不是“点射域”;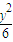 +
+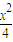 =1内部的向量构成的区域,
=1内部的向量构成的区域,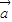 =(1,1)∈M,但3
=(1,1)∈M,但3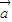 =(3,3)∉M,故它不是“点射域”.
=(3,3)∉M,故它不是“点射域”.

科目:高中数学 来源: 题型:
| a |
| a |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013年高考数学复习卷C(八)(解析版) 题型:填空题
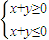 };
};查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com