

图1-1-23
科目:高中数学 来源: 题型:
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.1 1 |
| 2 |
| π |
| 4 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•滨州一模)我市某商场在春节促销活动中,对2011年2月2日10时至15时的销售额进行统计,其频率分布直方图如图所示,已知10时至11时销售额为3万元,则11时至13时的销售额为
(2011•滨州一模)我市某商场在春节促销活动中,对2011年2月2日10时至15时的销售额进行统计,其频率分布直方图如图所示,已知10时至11时销售额为3万元,则11时至13时的销售额为查看答案和解析>>
科目:高中数学 来源: 题型:
 A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.
A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.| 1 |
| 1 |
| 1 |
| 1×2 |
| 1 |
| 1×2×3 |
| 1 |
| 1×2×3×L×n |
查看答案和解析>>
科目:高中数学 来源: 题型:
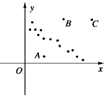 以下关于线性回归的判断,正确的有( )个.
以下关于线性回归的判断,正确的有( )个.| ? |
| y |
| A、0个 | B、1个 | C、2个 | D、3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com