
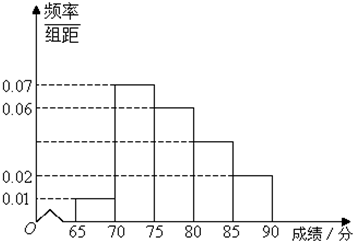
某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩分组如下:第一组[65,70),第二组 [70,75),第三组[75,80),第四组 [80,85),第五组 [85,90)(假设考试成绩均在[65,90)内),得到频率分布直方图如图:

(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组同学中用分层抽样的方法抽取6名同学组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有一名同学被抽中的的概率.
(1)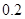 ;(2)
;(2)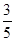 .
.
【解析】
试题分析:(1)由所有频率的和为 ,易得测试成绩在[80,85)内的频率;(2)先分别求出第三组、第四组、第五组的人数,再由分层抽样方法得各组应该抽取的人数。用字母表示所研究的事件,用列举法得基本事件的总数以及所研究事件含多少个基本事件,最后利用古典概型公式求得概率.
,易得测试成绩在[80,85)内的频率;(2)先分别求出第三组、第四组、第五组的人数,再由分层抽样方法得各组应该抽取的人数。用字母表示所研究的事件,用列举法得基本事件的总数以及所研究事件含多少个基本事件,最后利用古典概型公式求得概率.
试题解析:(1)测试成绩在[80,85)内的频率为: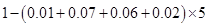 2分
2分
 3分
3分
(2)第三组的人数等于 ,第四组的人数等于
,第四组的人数等于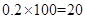 ,
,
第五组的人数等于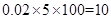 ,
5分
,
5分
分组抽样各组的人数为第三组3人,第四组2人,第五组1人. 6分
设第三组抽到的3人为 ,第四组抽到的2人为
,第四组抽到的2人为 ,第五组抽到的1人为
,第五组抽到的1人为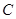 . 7分
. 7分
这6名同学中随机选取2名的可能情况有15种,如下:

 . 10分
. 10分
设“第四组2名同学至少有一名同学被抽中”为事件 ,事件
,事件 包含的事件个数有9种,即:
包含的事件个数有9种,即:


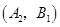 ,
,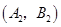 ,
,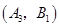 ,
,
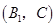 ,
,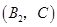 .
11分
.
11分
所以, 事件 的概率即第四组至少有一名同学被抽中的概率为
的概率即第四组至少有一名同学被抽中的概率为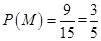 .
12分
.
12分
考点:1、考查频率分布;2、频率分布直方图;3、古典概型.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011年福建省高二上学期期末考试数学理卷 题型:选择题
为落实素质教育,某中学拟从4个重点研究性课题和6个一般研究性课题中各选2个课题作为本年度该校启动的课题项目,若重点研究性课题A和一般研究性课题 中至少有一个被选中的不同选法种数是
中至少有一个被选中的不同选法种数是 ,那么二项式
,那么二项式 的展开式中
的展开式中 的系数为
的系数为
A.50000 B.54000 C.56000 D.59000
查看答案和解析>>
科目:高中数学 来源: 题型:
为落实素质教育,某中学拟从4个重点研究性课题和6个一般研究性课题中各选2个课题作为本年度该校启动的课题项目,若重点研究性课题A和一般研究性课题![]() 中至少有一个被选中的不同选法种数是
中至少有一个被选中的不同选法种数是![]() ,那么二项式
,那么二项式![]() 的展开式中
的展开式中![]() 的系数为
的系数为
A.50000 B.54000 C.56000 D.59000
查看答案和解析>>
科目:高中数学 来源:安徽省08-09学年高二下学期六校联考(理) 题型:选择题
为落实素质教育,某中学拟从4个重点研究性课题和6个一般研究性课题中各选2个课题作为本年度该校启动的课题项目,若重点研究性课题A和一般研究性课题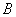 中至少有一个被选中的不同选法种数是
中至少有一个被选中的不同选法种数是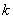 ,那么二项式
,那么二项式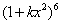 的展开式中
的展开式中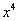 的系数为
的系数为
A.50000 B.54000 C.56000 D.59000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com