
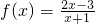 的图象关于点(1,2)成中心对称;
的图象关于点(1,2)成中心对称;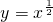 的图象始终在函数y=x的图象上方;
的图象始终在函数y=x的图象上方;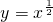 的图象始终在函数y=x的图象下方;④利用函数的定义,即一个x只能有一个y值与之对应,可判断④的真假
的图象始终在函数y=x的图象下方;④利用函数的定义,即一个x只能有一个y值与之对应,可判断④的真假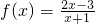 =
=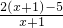 =2-
=2-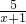 ,此函数是由反比例函数y=-
,此函数是由反比例函数y=- 向左平移一个单位,再向上平移2个单位得到的,由反比例函数的对称中心为(0,0)知,此函数的对称中心为(-1,2),故②错误;
向左平移一个单位,再向上平移2个单位得到的,由反比例函数的对称中心为(0,0)知,此函数的对称中心为(-1,2),故②错误;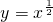 的图象与函数y=x的图象的两个交点,且
的图象与函数y=x的图象的两个交点,且
 ,故③错误;
,故③错误;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| ax+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2-1 |
| 1-x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:022
给出下列几个命题,其中正确命题的序号为________.
①若空间两直线与第三条直线所成的角相等,则这两条直线平行
②如果空间两平面都垂直于第三个平面,那么这两个平面平行
③空间中,到一定点的距离等于定长的轨迹是球
④正三棱锥两侧面所成的二面角大于60°
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:022
①若空间两直线与第三条直线所成的角相等,则这两条直线平行
②如果空间两平面都垂直于第三个平面,那么这两个平面平行
③空间中,到一定点的距离等于定长的轨迹是球
④正三棱锥两侧面所成的二面角大于60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com