分析:(Ⅰ)依题意得,y′=2x,于是可求曲线C在点M
n(a
n,
)处的切线方程为y=2a
n(x-a
n)+
,当n=1时,切线过点P(1,0),解得a
1=2;当n>1时,切线过点P
n-1(a
n-1,0),从而可得a
n与a
n-1(n≥2)的关系式;
(Ⅱ)由(Ⅰ)知数列{a
n}的通项公式为a
n=2
n,而b
n=
,S
n=
+
+
+…+
,利用错位相减法即可求得数列{b
n}的前n项和.
解答:解:(Ⅰ)对y=x
2求导,得y′=2x,
∴曲线C在点M
n(a
n,
)处的切线方程是y=2a
n(x-a
n)+
,由已知得a
n>0,
当n=1时,切线过点P(1,0),
∴2a
1(1-a
1)+
=0,解得a
1=2;
当n>1时,切线过点P
n-1(a
n-1,0),
同理可得得a
n=2a
n-1,
∴数列{a
n}是首项a
1=2,公比q=2的等比数列,
∴数列{a
n}的通项公式为a
n=2
n.
(Ⅱ)∵a
n=2
n,b
n=
,
∴S
n=
+
+
+…+
①,
∴
S
n=
+
+
+…+
②,
①-②得:
S
n=
+
+…+
-
=
-
=1-
-
,
∴S
n=2-
.
点评:本题考查数列的求和,着重考查利用导数研究曲线上某点切线方程,考查等比数列关系的确定及通项公式的应用,突出考查错位相减法求和,属于中档题.



 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案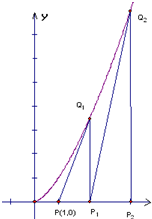 如图,过点P(1,0)作曲线C:y=xk(x∈(0,+∞),k∈N*,k>1)的切线,切点为Q1,设Q1点在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an.
如图,过点P(1,0)作曲线C:y=xk(x∈(0,+∞),k∈N*,k>1)的切线,切点为Q1,设Q1点在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an.

 (2009•锦州一模)过点P(1,0)作曲线C:y=x2(x>0)的切线,切点为Q1,没Q1在x轴上的投影是P1,又过P1,作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2…,依次下去,得到一系列点Q1Q2,…Qn,设Qn的横坐标为an.
(2009•锦州一模)过点P(1,0)作曲线C:y=x2(x>0)的切线,切点为Q1,没Q1在x轴上的投影是P1,又过P1,作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2…,依次下去,得到一系列点Q1Q2,…Qn,设Qn的横坐标为an.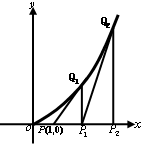 (2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.
(2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.