练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数且函数f(x)在区间(－1，1)上单调递增，在区间(1，3)上单调递减．

    (1)

    若b＝－2，求c的值；

    (2)

    求证：c≥3；

    (3)

    设函数的最小值是－1，求b、c的值

    答案：
    解析：

    (1)

    解：由已知可得f‘(1)＝0…………………………………………………………1分

    又

    f‘(1)＝1＋2b＋c＝0，………………………………………………………………2分

    将b＝－2代入，可得c＝3………………………………………………………………3分

    (2)

    解：可知

    令……………………………………………………4分

    又当－1＜x＜1时，

    如图所示；

    易知c≥3…………………………8分

    (3)

    解：若1≤－b≤3，则

    又1＋2b＋c＝0，得b＝－2或b＝0(舍)，c＝3，

    若－b≥3，则

    ＝9＋6b＋c＝－1，又1＋2b＋c＝0

    得(舍)

    综上所述，b＝－2，c＝3…………………………………………14分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2010-2011年安徽省安庆市示范高中高一三校联考数学试卷 题型：解答题

    已知函数 且此函数图象过点（1，5）.（1）求实数m的值；  （2）判断f(x)奇偶性；(3)讨论函数f(x)在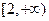上的单调性？并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年北京市高三下学期开学检测文科数学试卷 题型：解答题

    （本小题满分12分）

    已知函数且函数f(x)的最小正周期为.

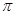    （1）求函数f(x)的解析式；

    （2）在△ABC中，角A，B，C所对的边分别为a，b，c.若f(B)=1，且，试求的值.

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年安徽省安庆市高一三校联考数学试卷 题型：解答题

    已知函数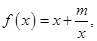 且此函数图象过点（1，5）.（1）求实数m的值；   （2）判断f(x)奇偶性；(3)讨论函数f(x)在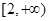上的单调性？并证明你的结论.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2013届安徽省安庆市三校联考高一上学期期末考试数学 题型：解答题

    已知函数 且此函数图象过点（1， 5）.（1）求实数m的值；   （2）判断f(x)奇偶性；(3)讨论函数f(x)在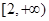上的单调性？并证明你的结论.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (理)已知函数f(x)=xlnx.

    (1)求函数f(x)的单调区间和最小值;

    (2)当b＞0时，求证:bb≥(其中e=2.718 28…是自然对数的底数);

    (3)若a＞0,b＞0，证明f(a)+(a+b)ln2≥f(a+b)-f(b).

    (文)已知向量m=(x2,y-cx),n=(1,x+b)(x,y,b,c∈R)且m∥n,把其中x,y所满足的关系式记为y=f(x).若f′(x)为f(x)的导函数,F(x)=f(x)+af′(x)(a＞0),且F(x)是R上的奇函数.

    (1)求和c的值.

    (2)求函数f(x)的单调递减区间(用字母a表示).

    (3)当a=2时,设0＜t＜4且t≠2,曲线y=f(x)在点A(t,f(t))处的切线与曲线y=f(x)相交于点B(m,f(m))(A与B不重合),直线x=t与y=f(m)相交于点C,△ABC的面积为S,试用t表示△ABC的面积S(t),并求S(t)的最大值.

    查看答案和解析>>

    同步练习册答案